Måned: februar 2020

LS

Af

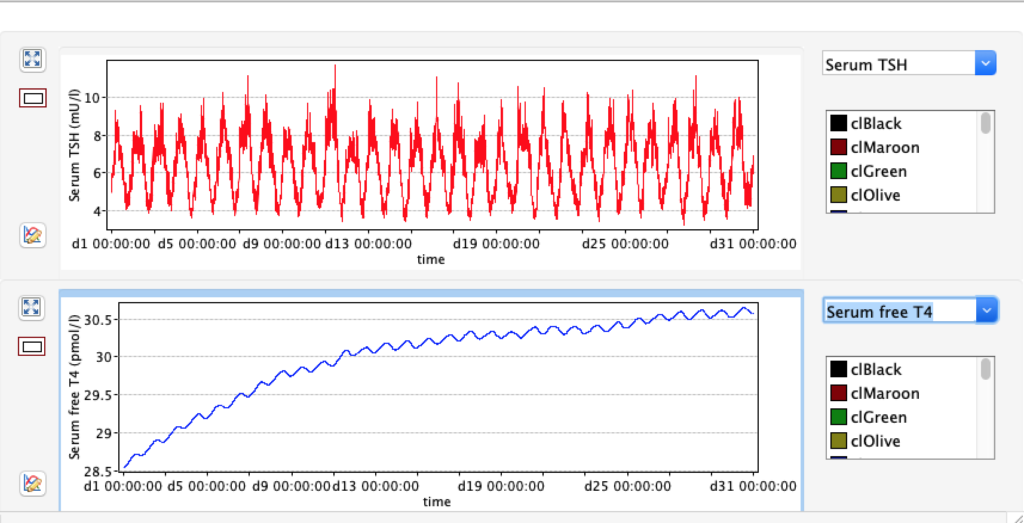
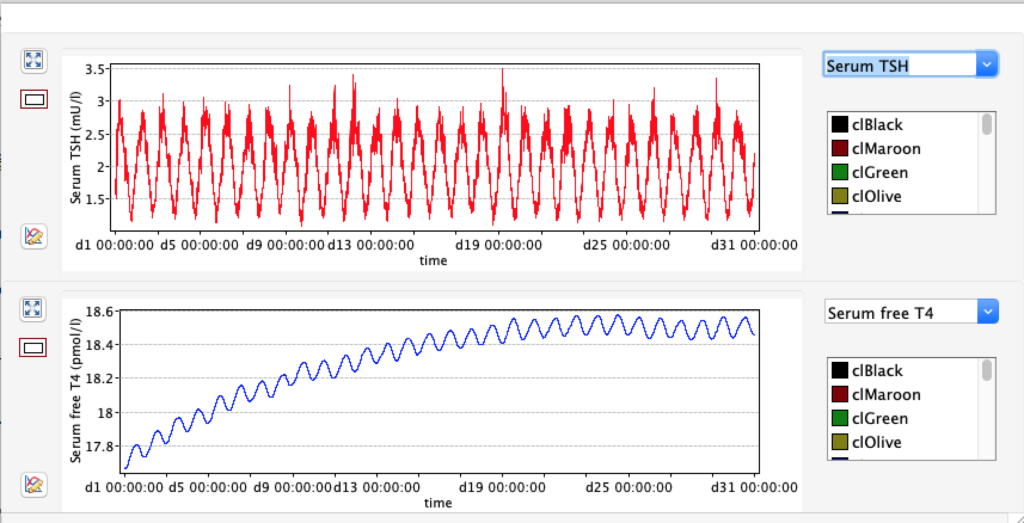
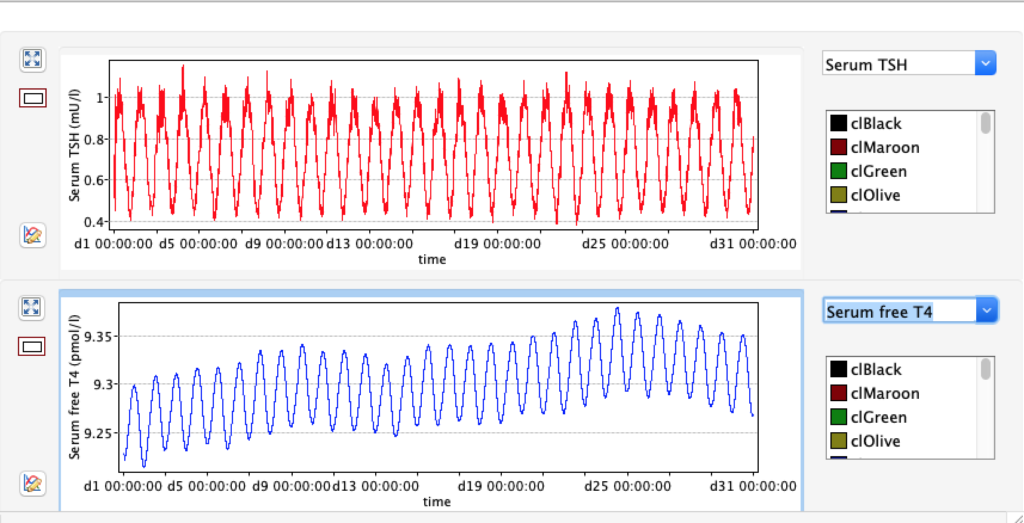
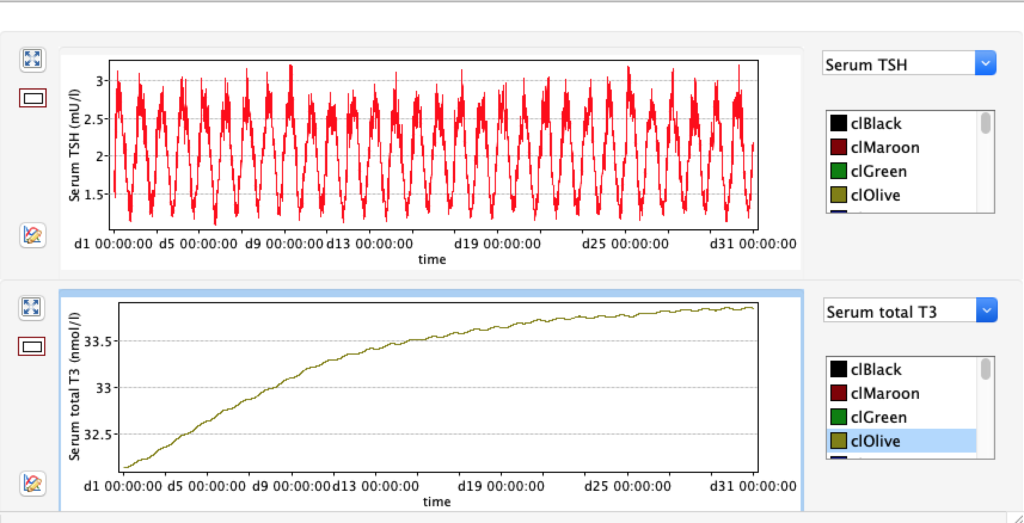
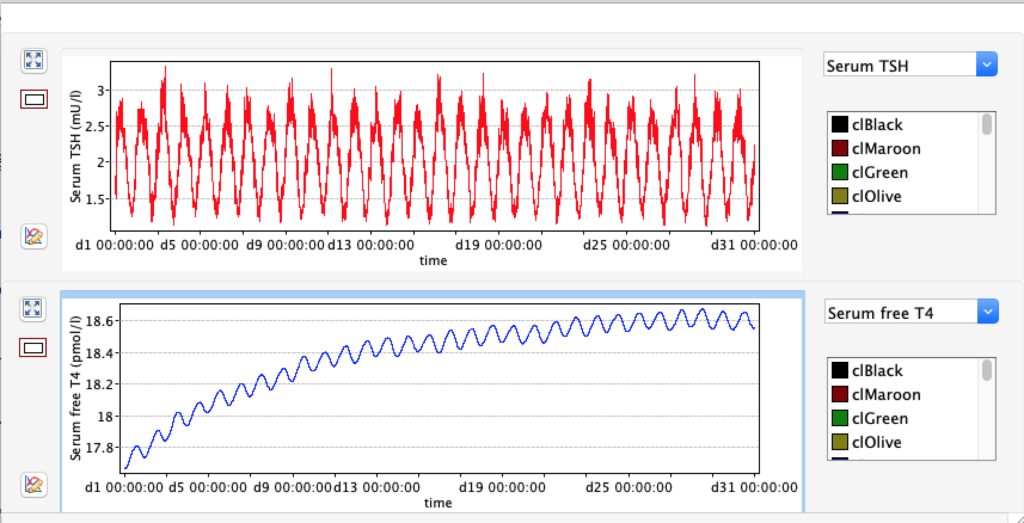
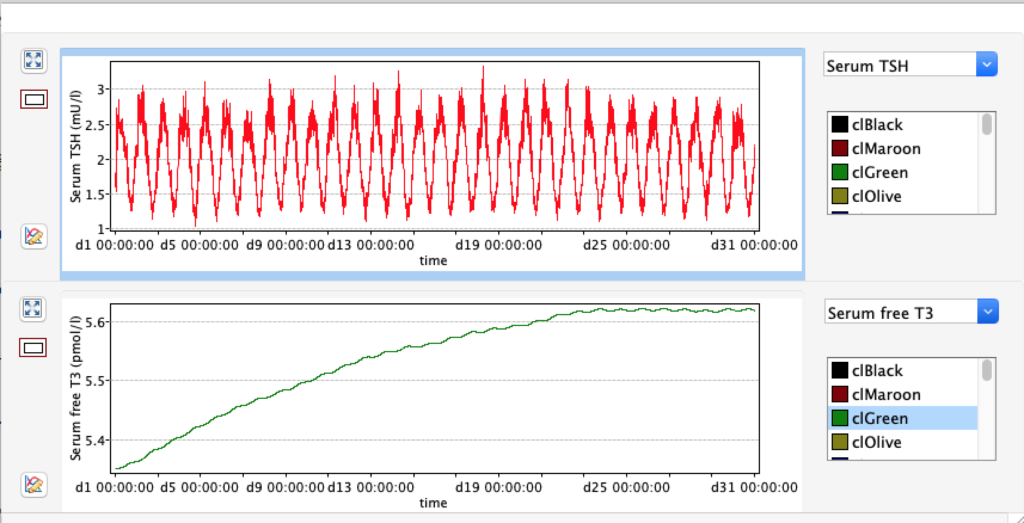
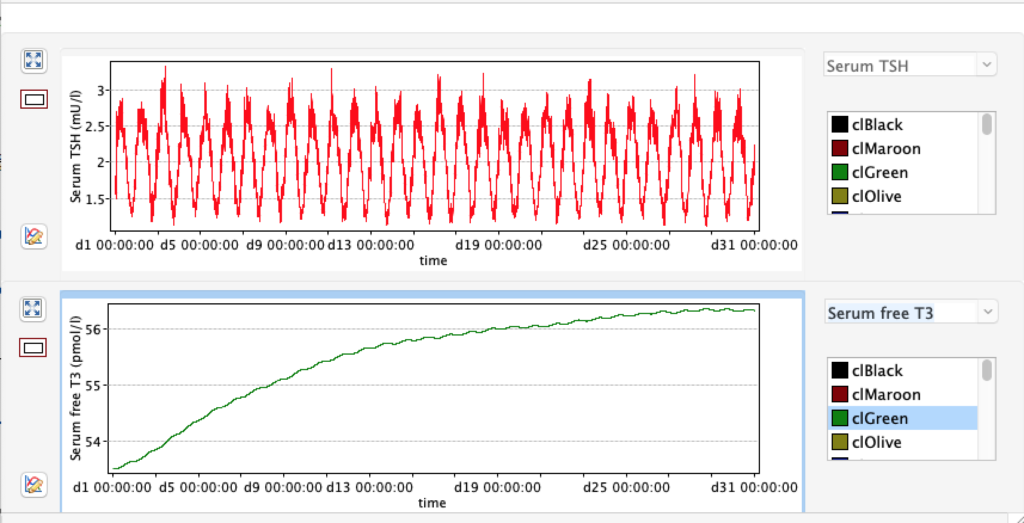
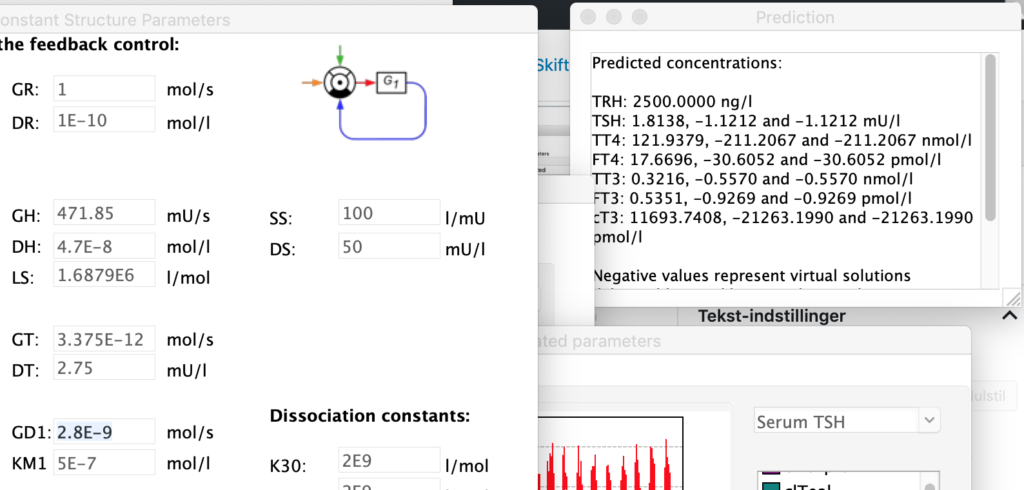
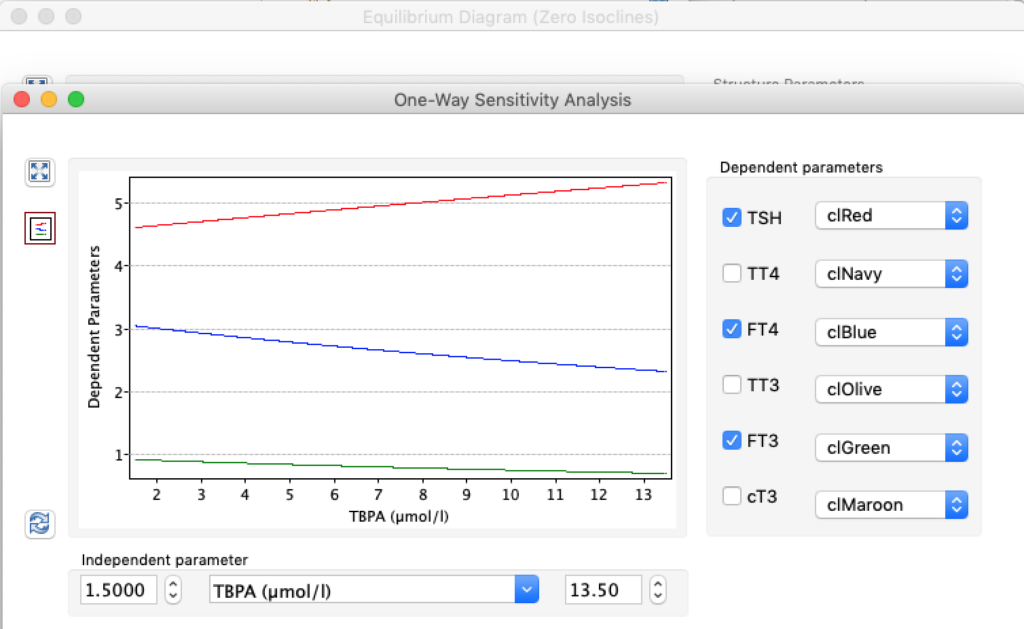
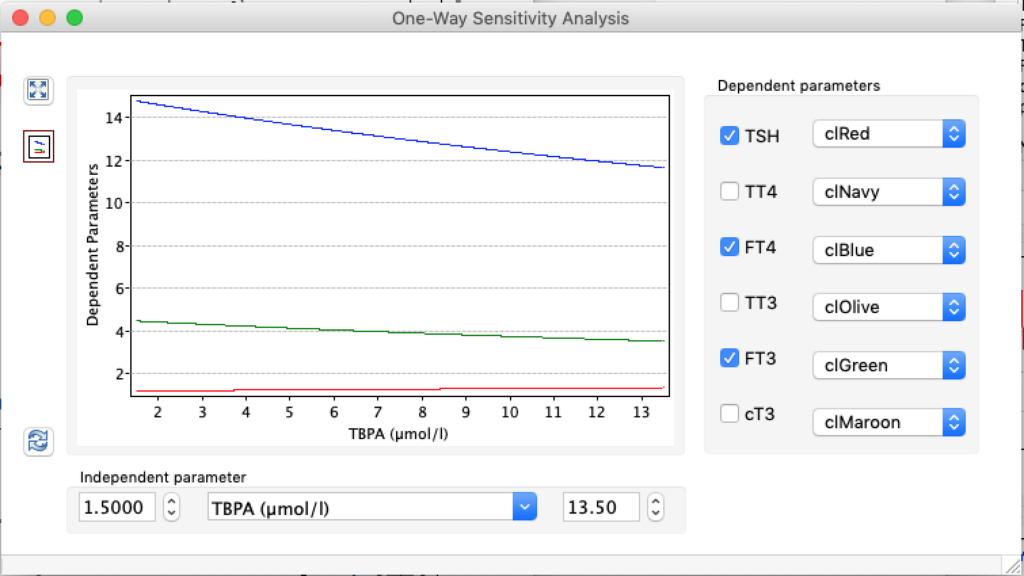
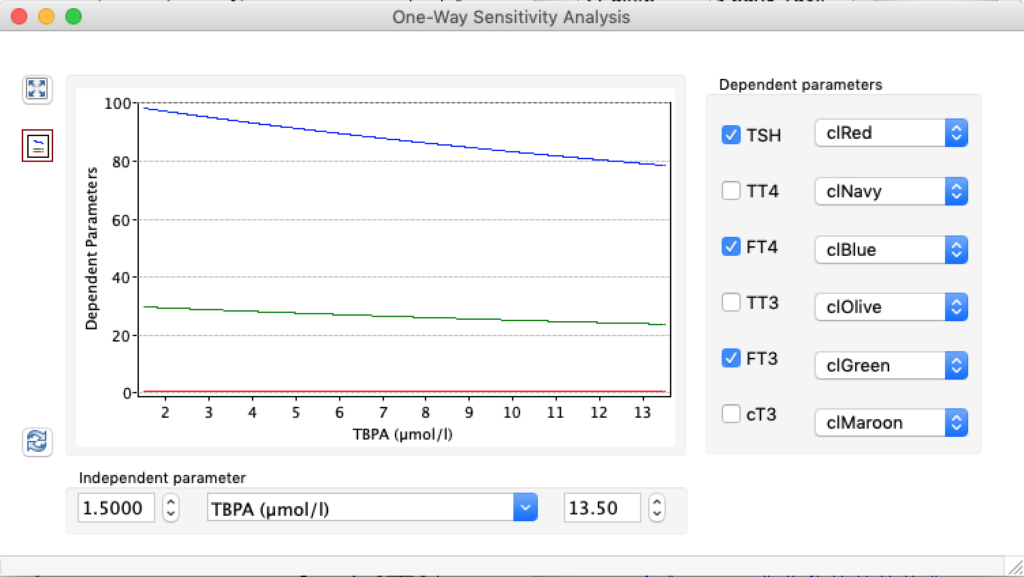
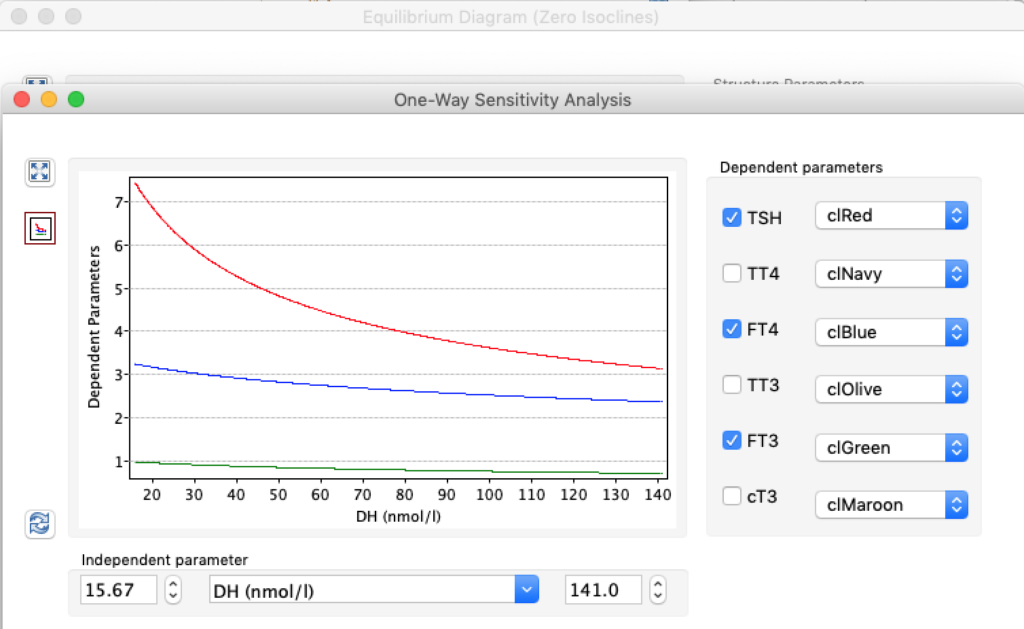
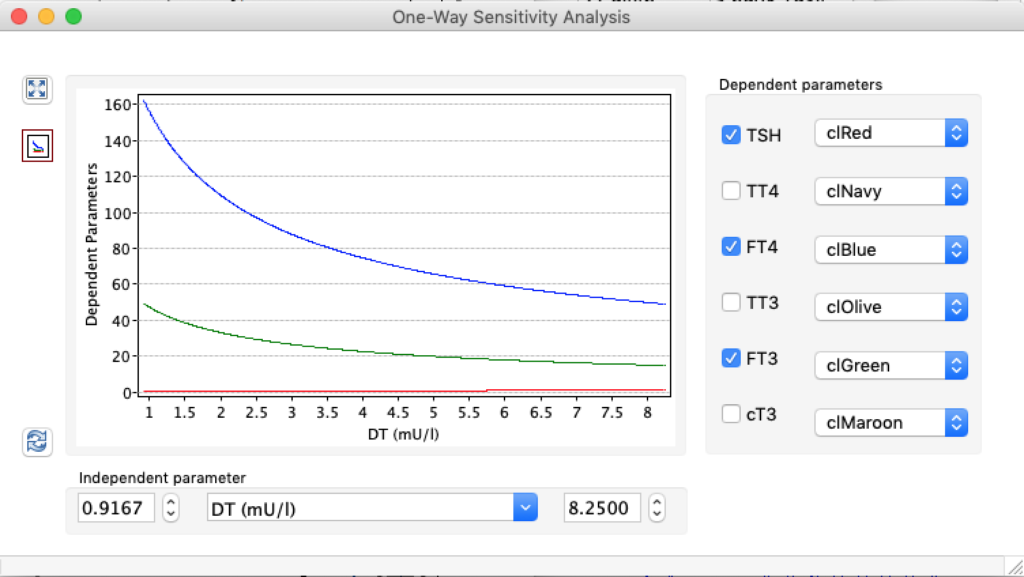
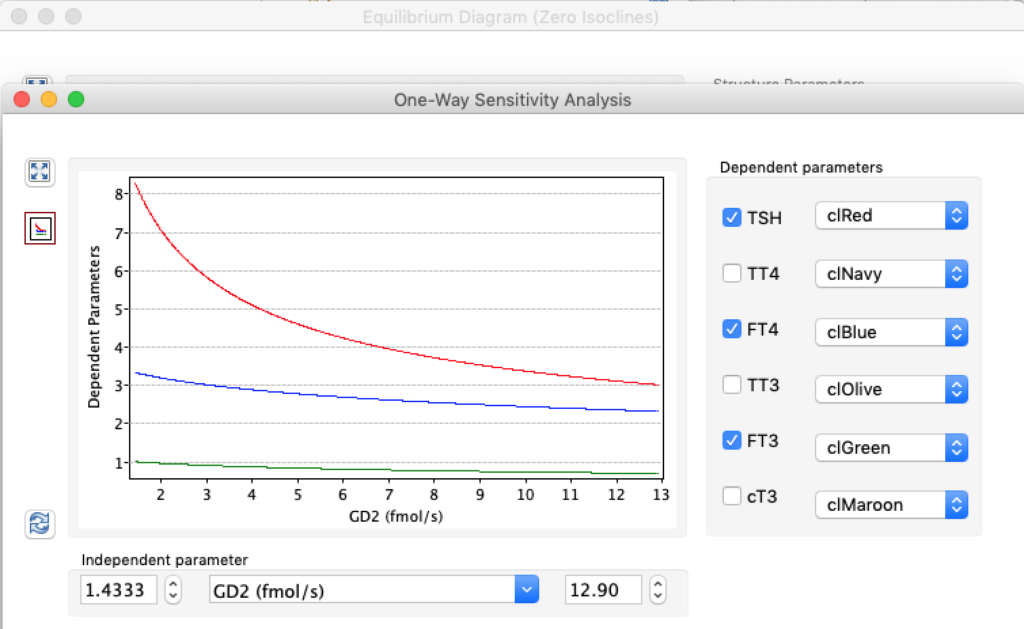
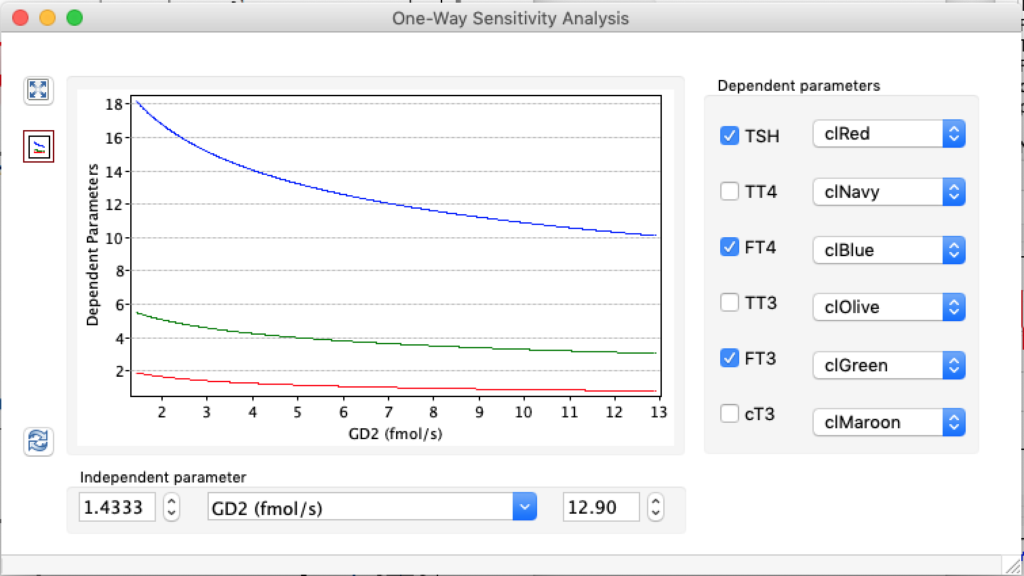
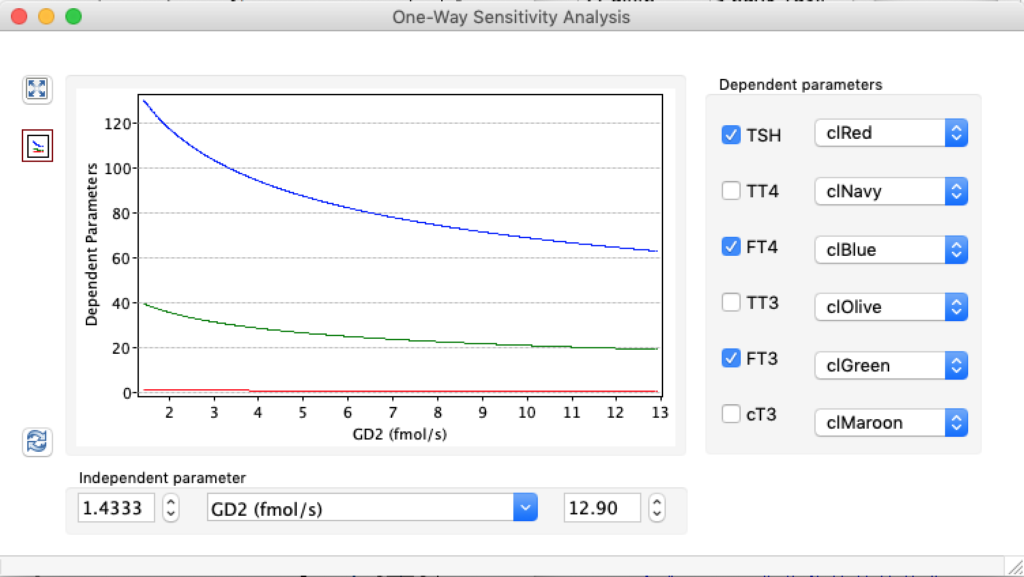
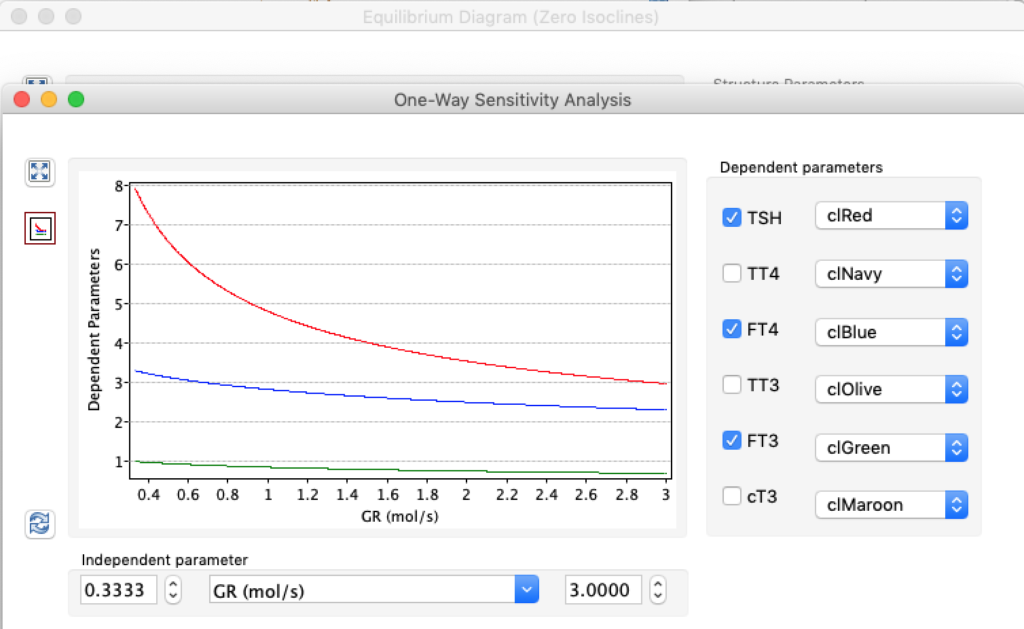
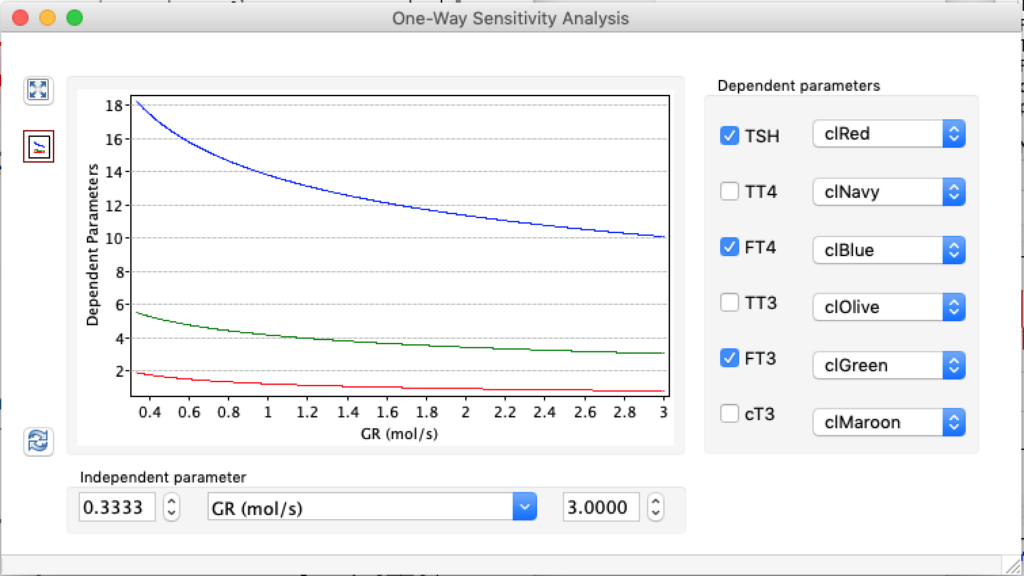
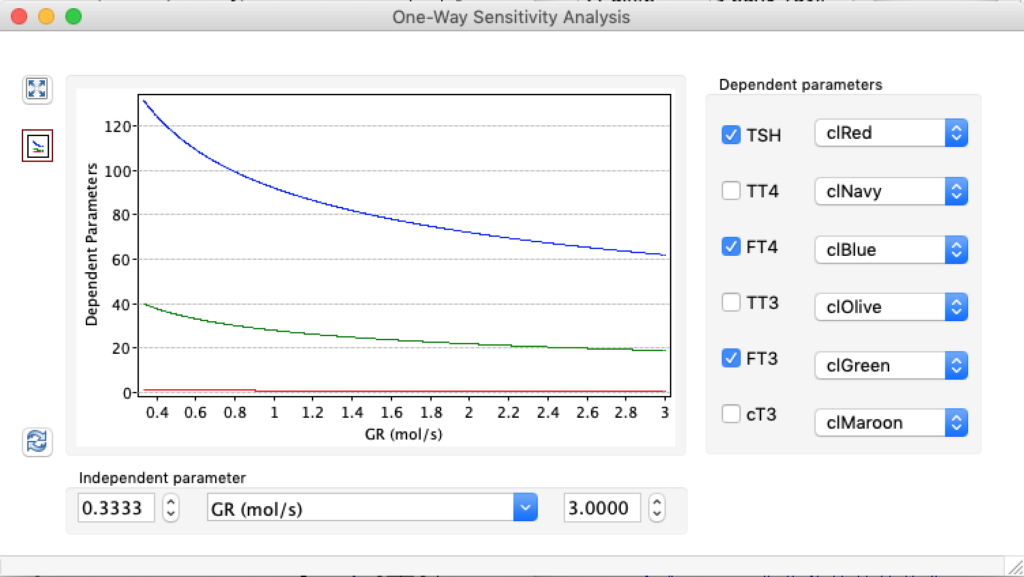
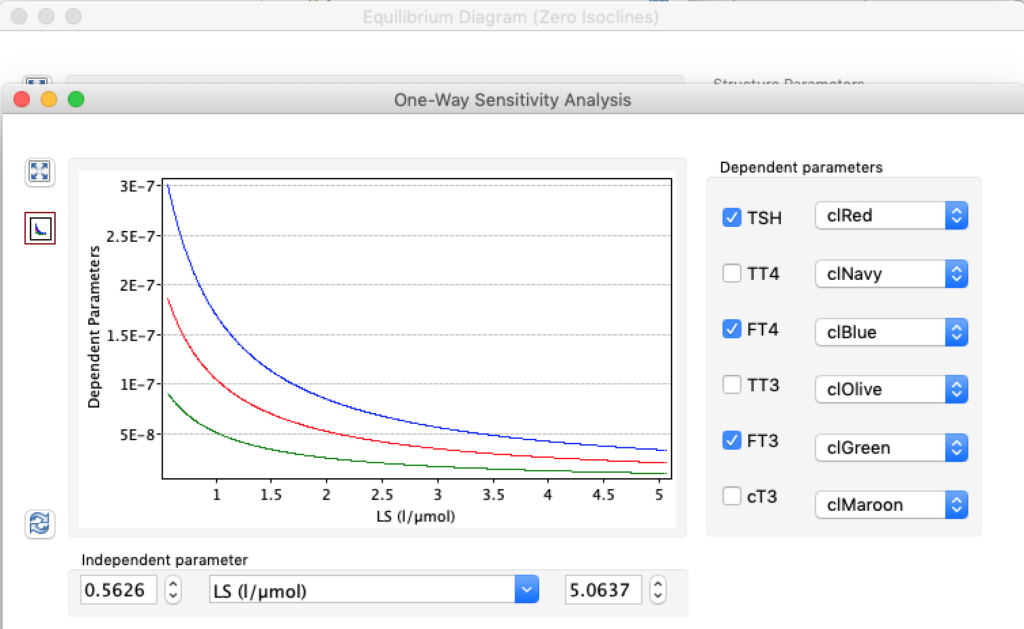
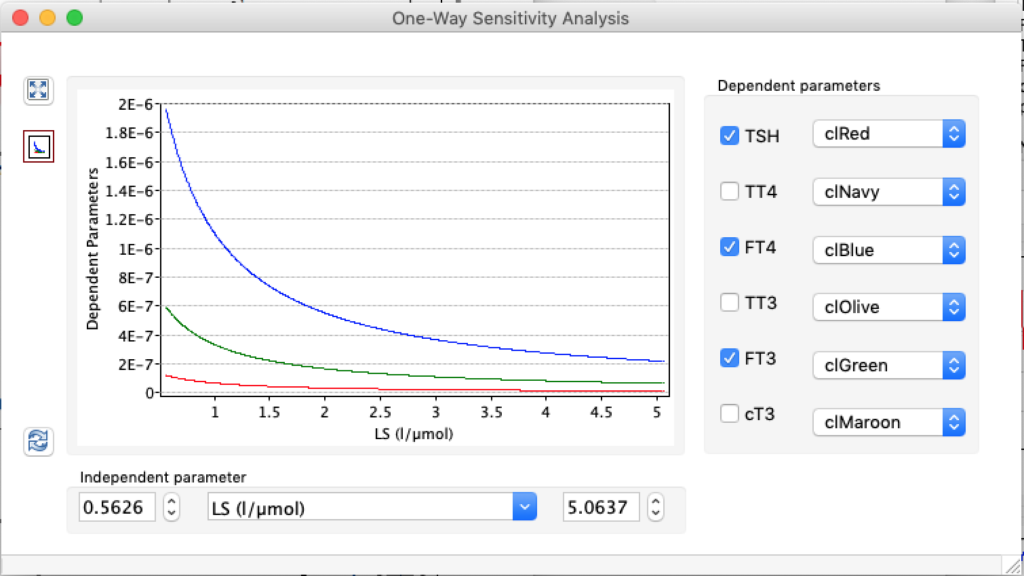
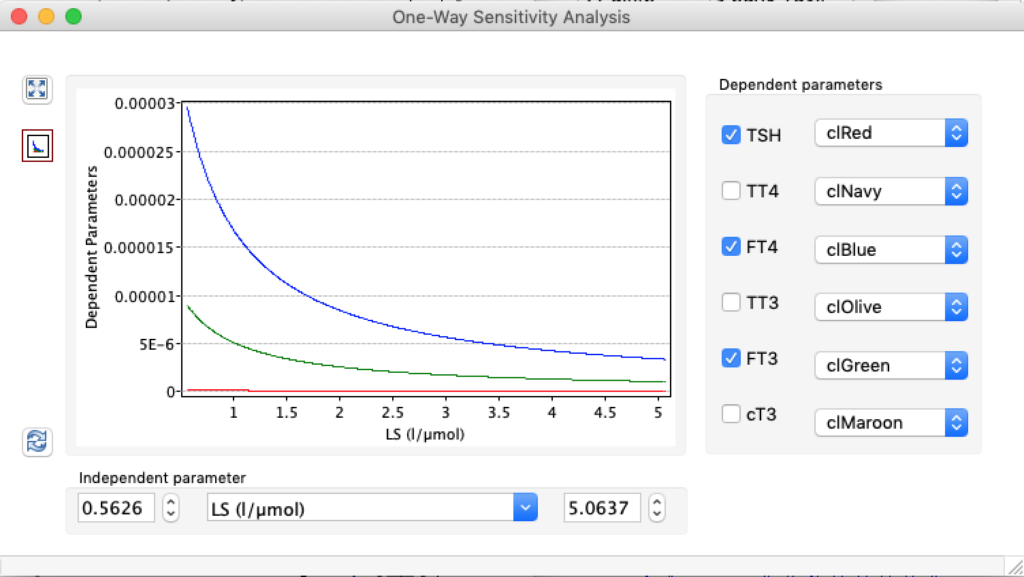
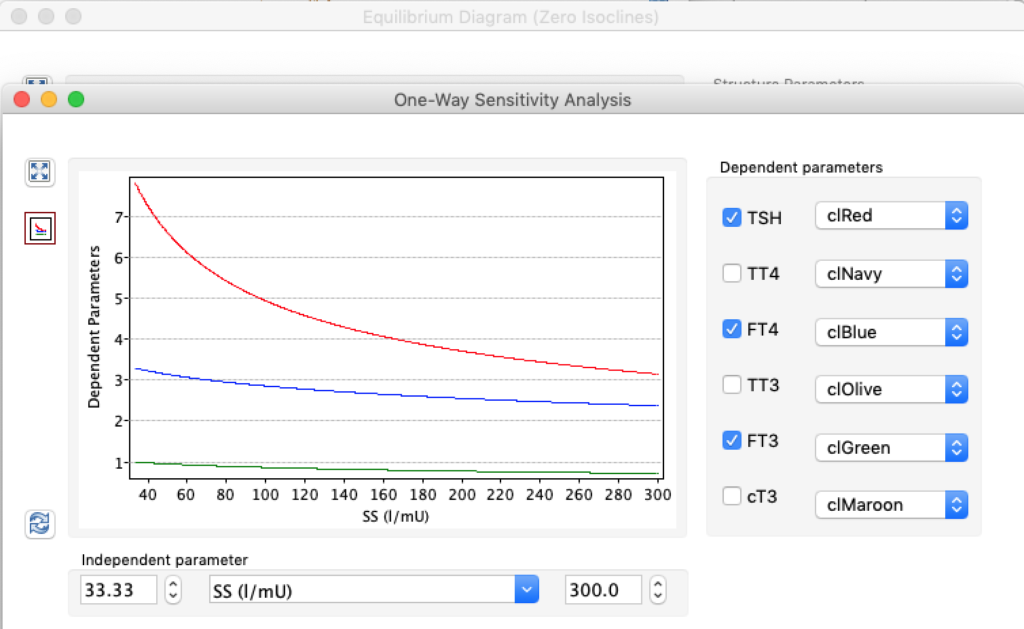
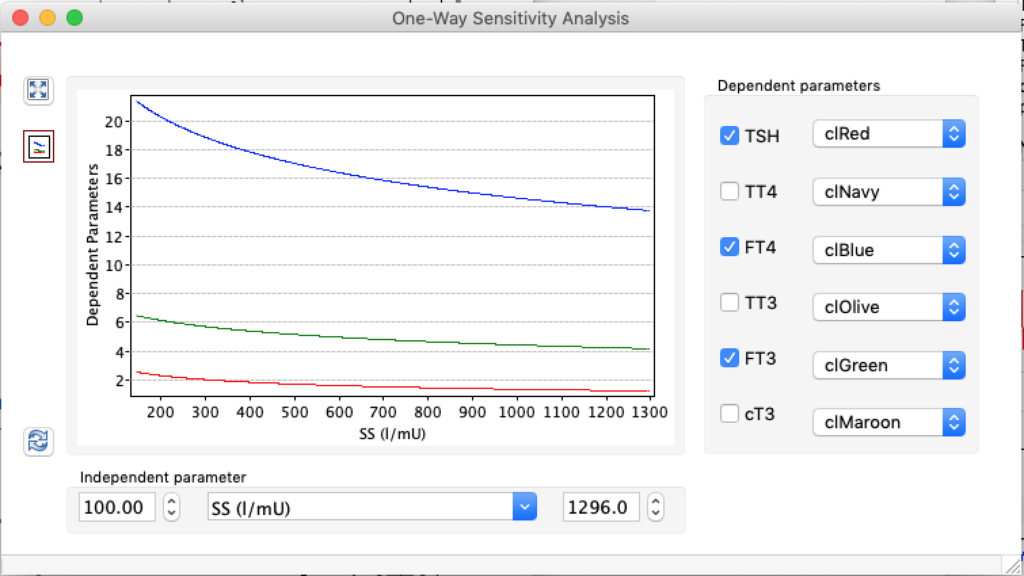
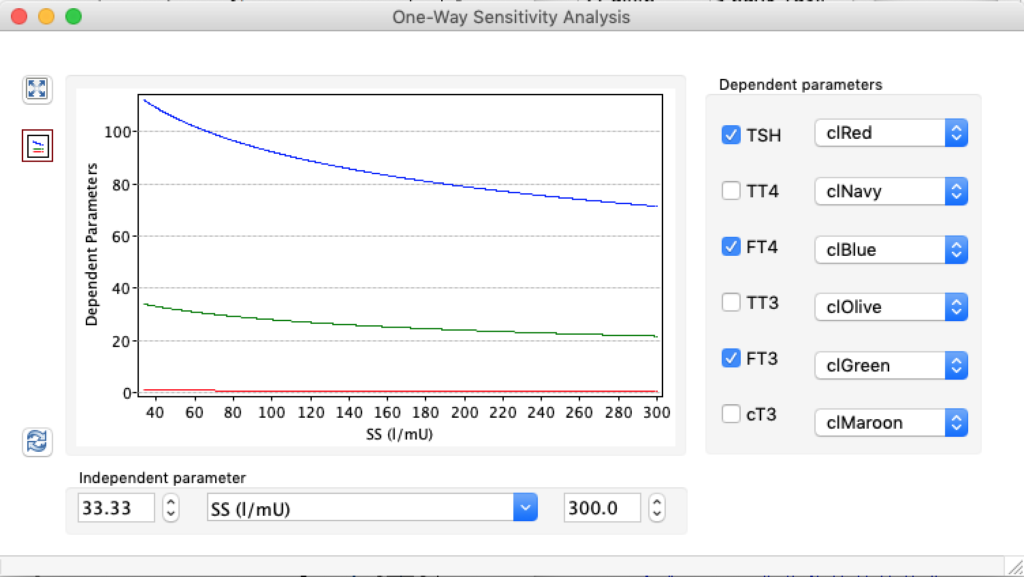
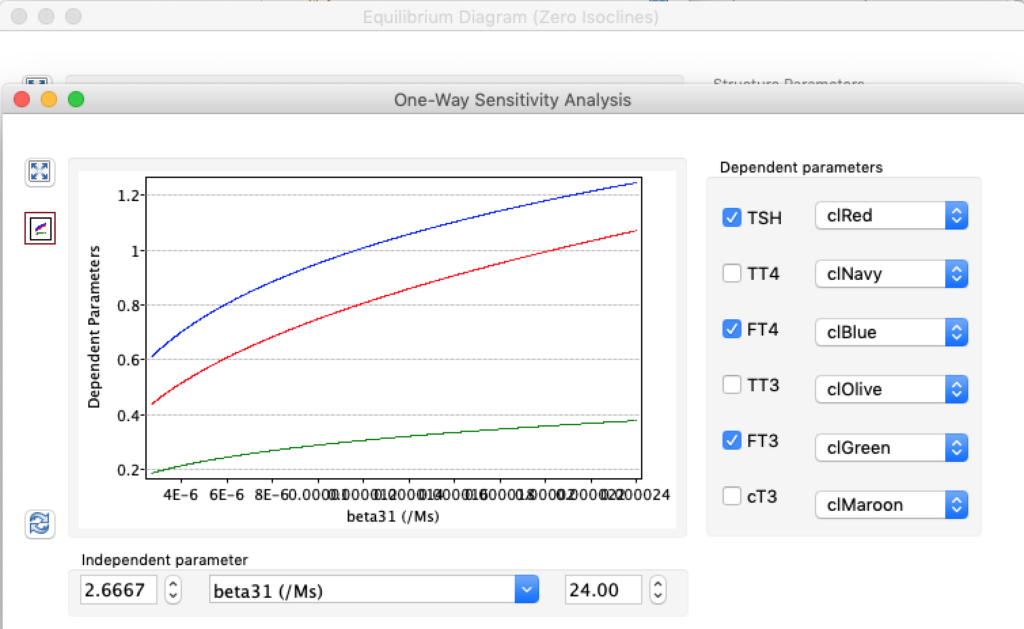
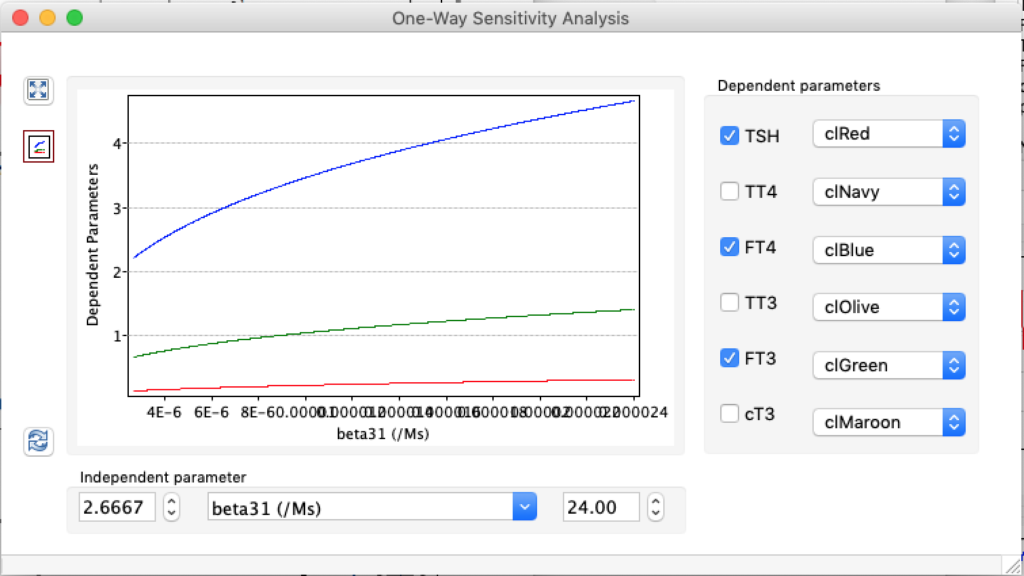
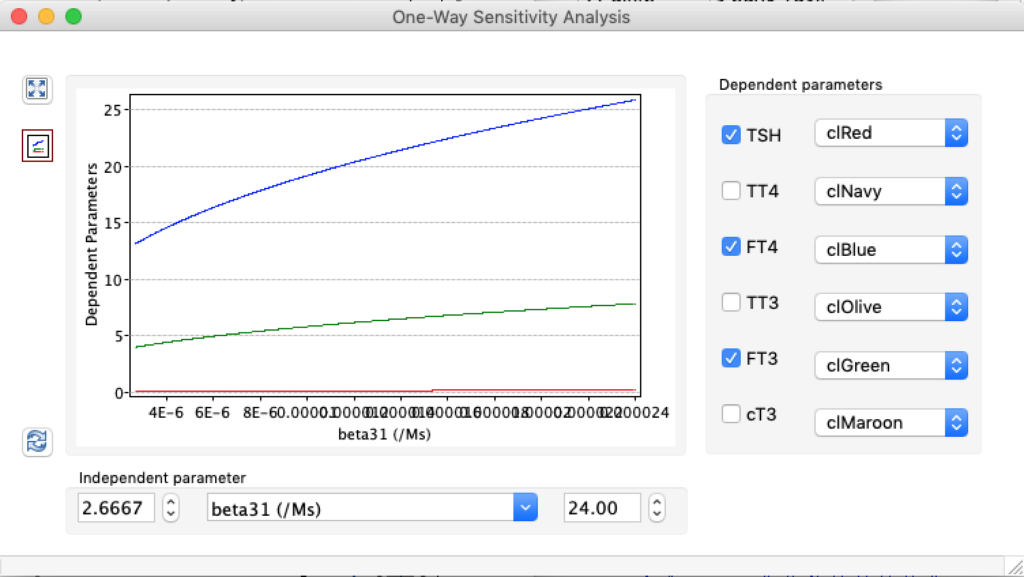
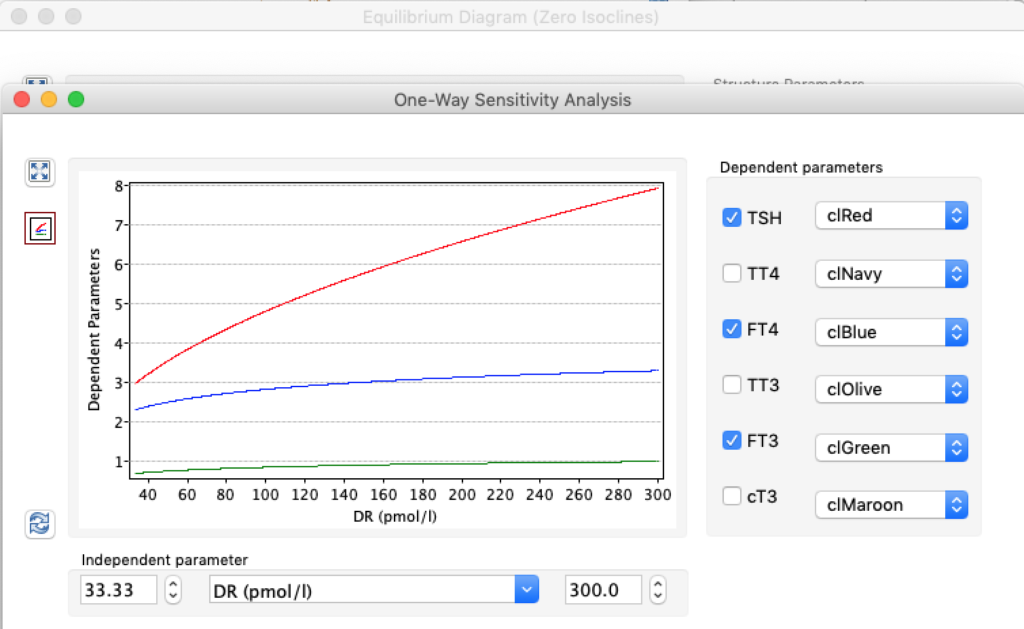
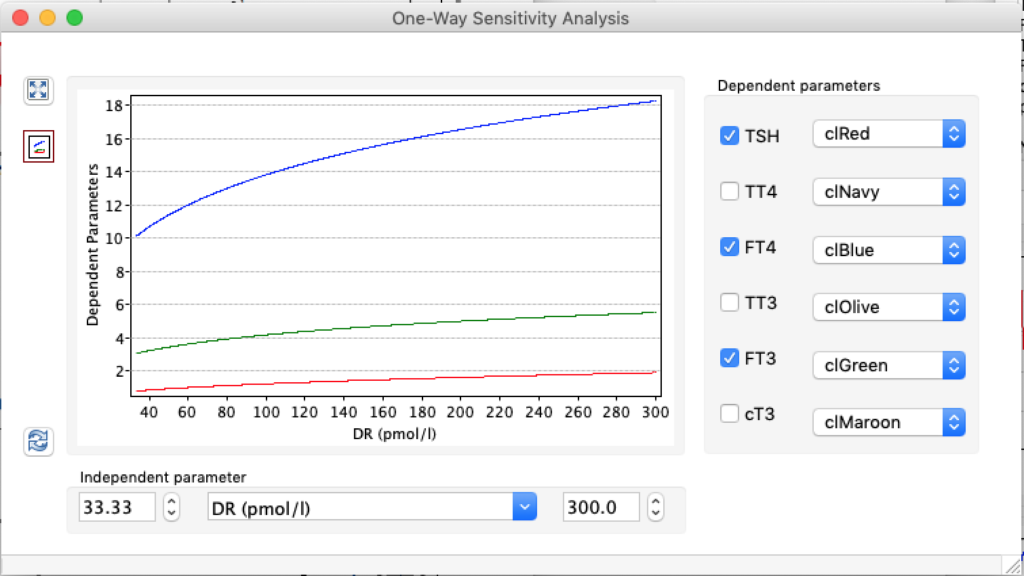
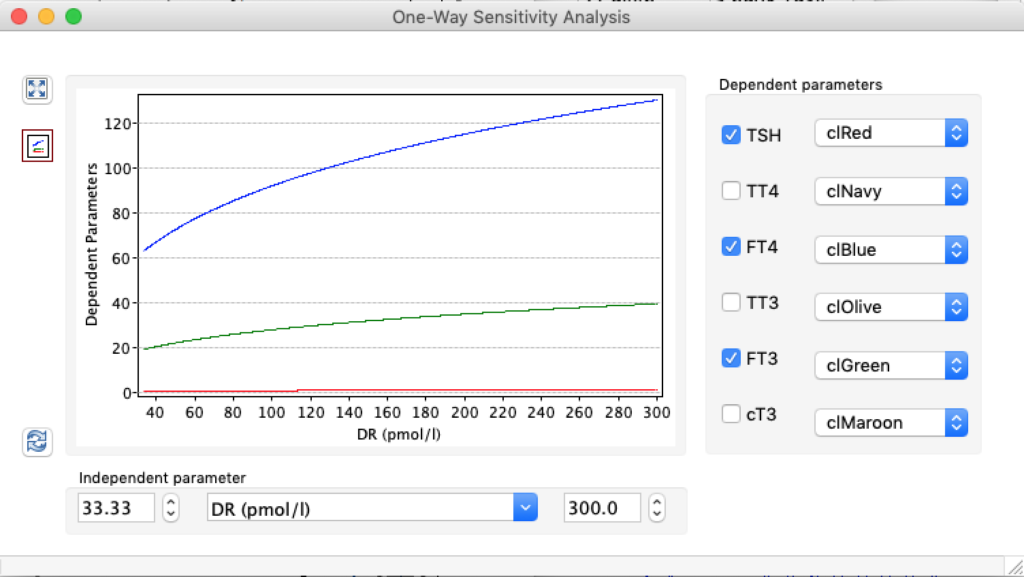
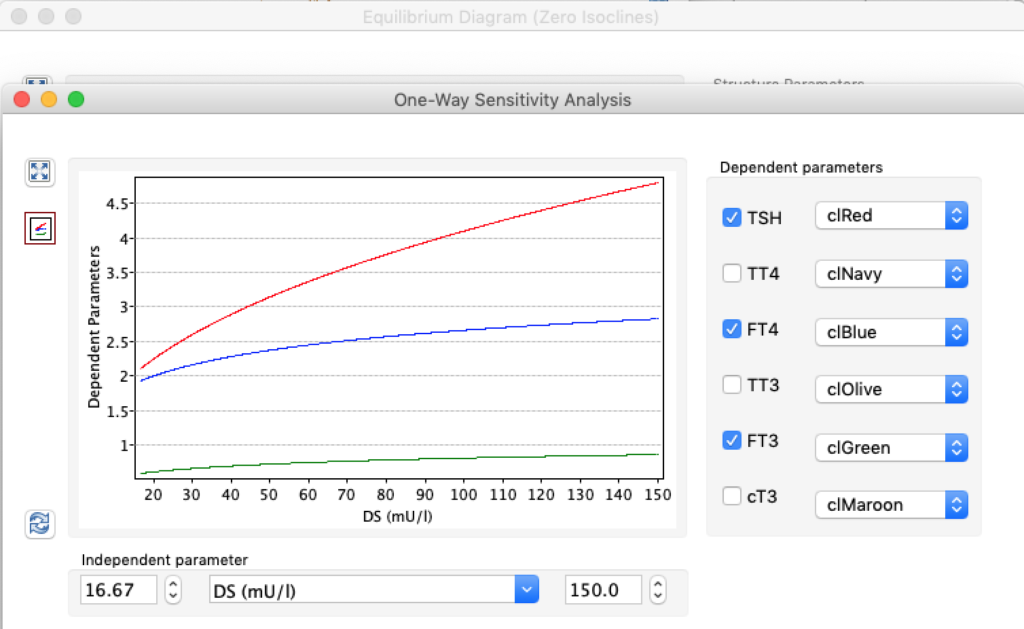
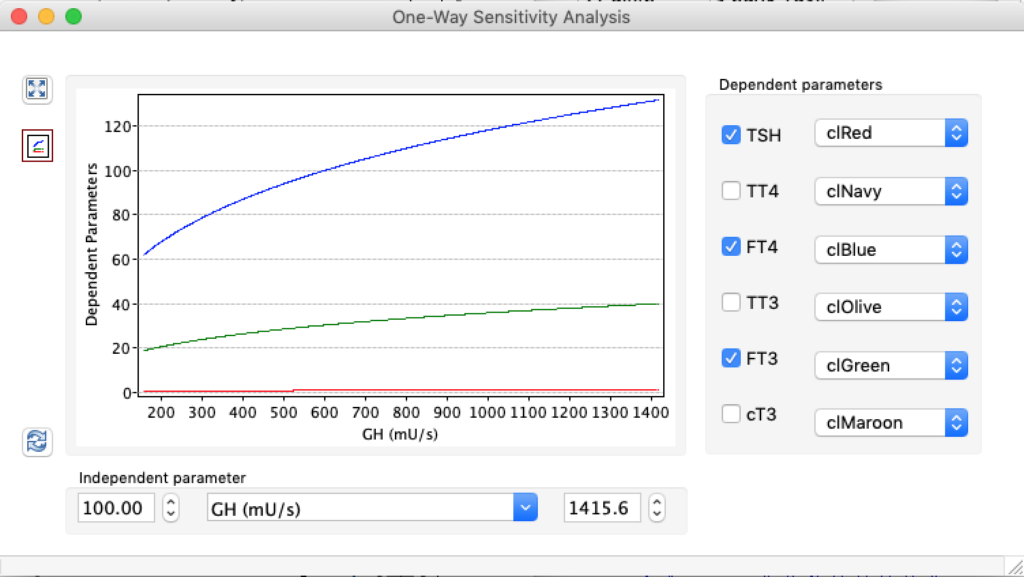
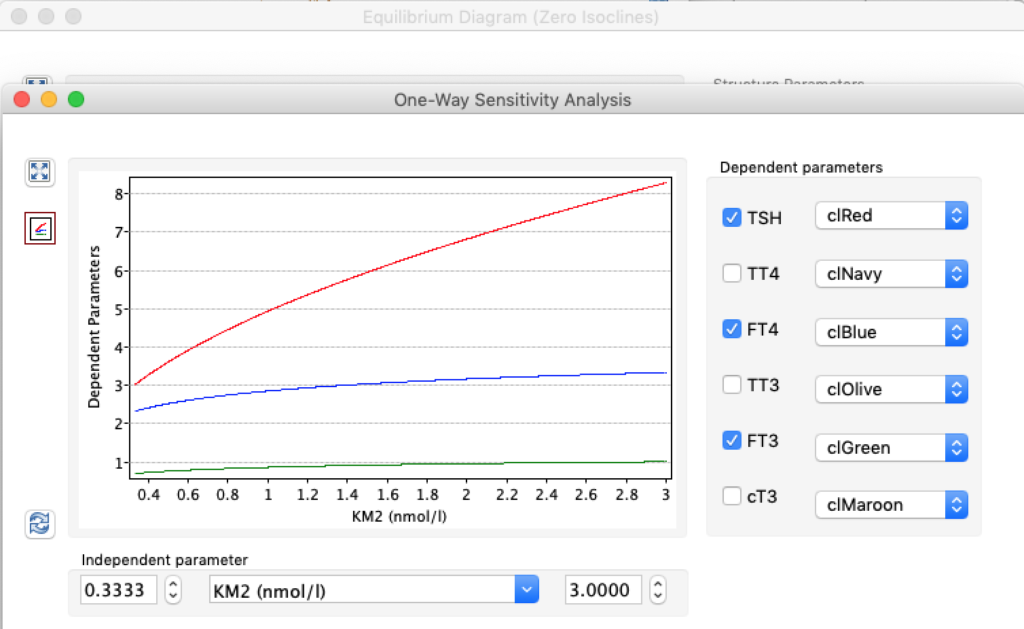
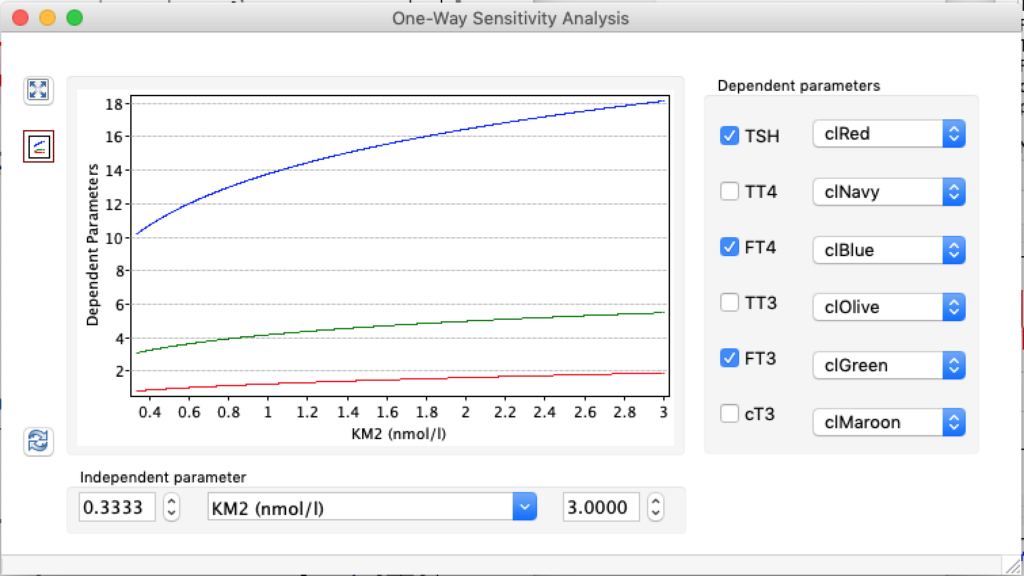
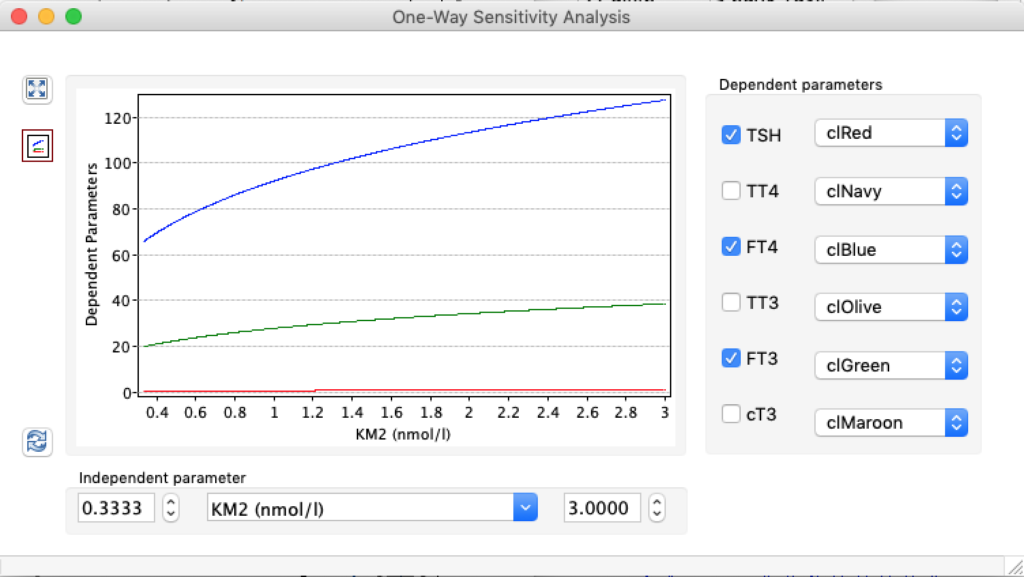
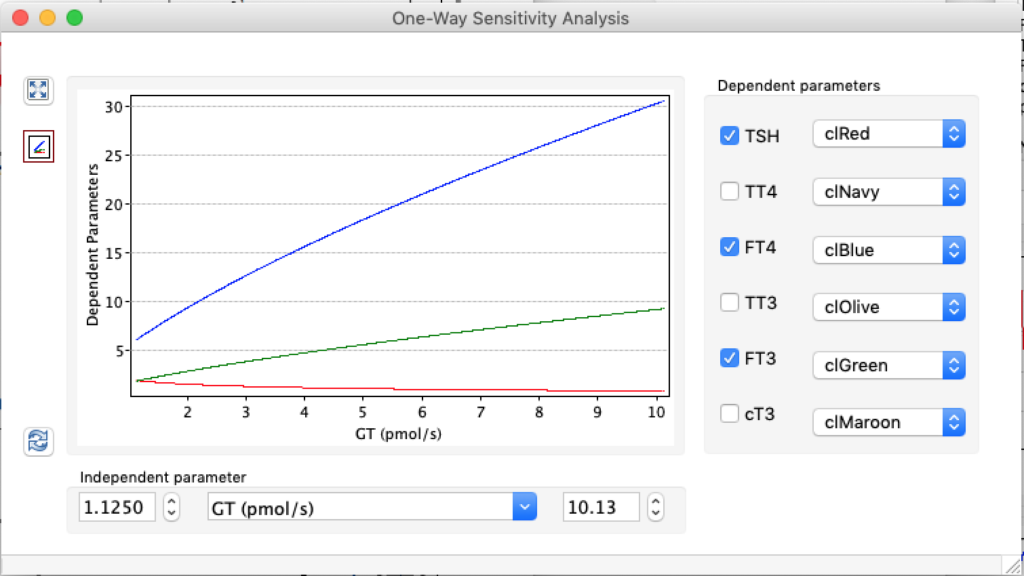
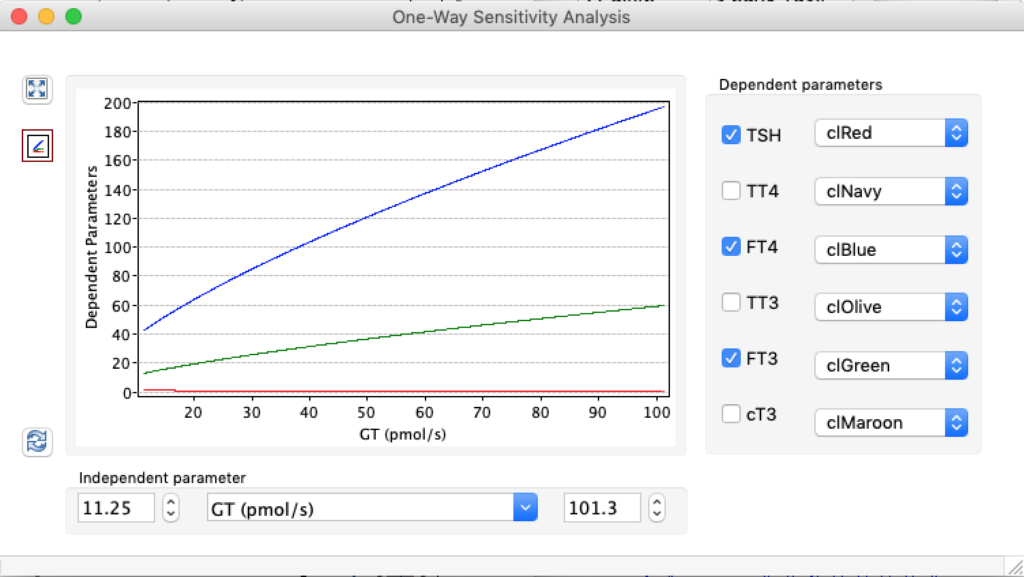
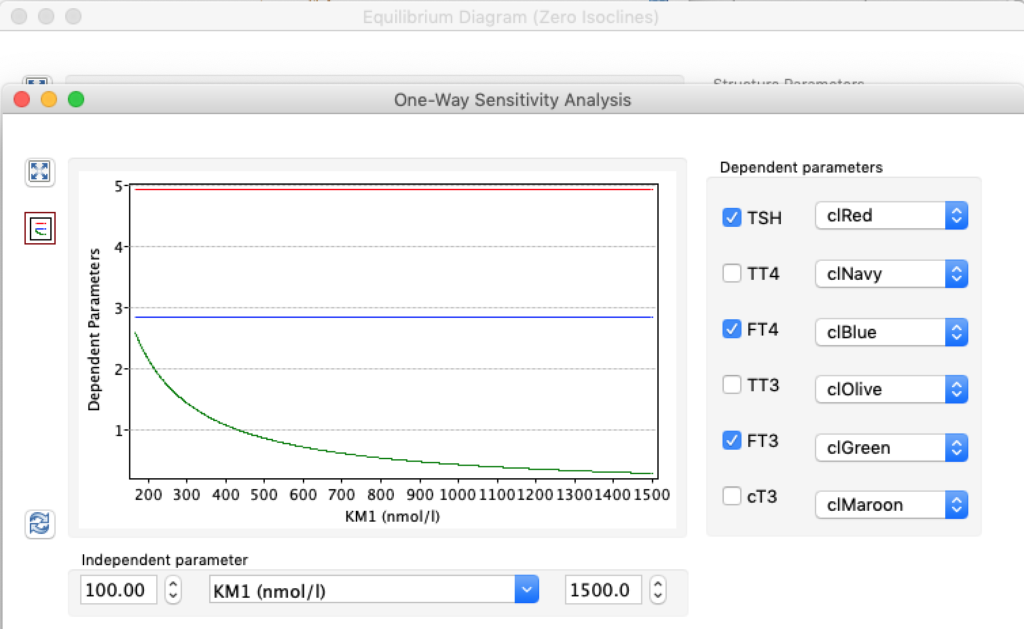
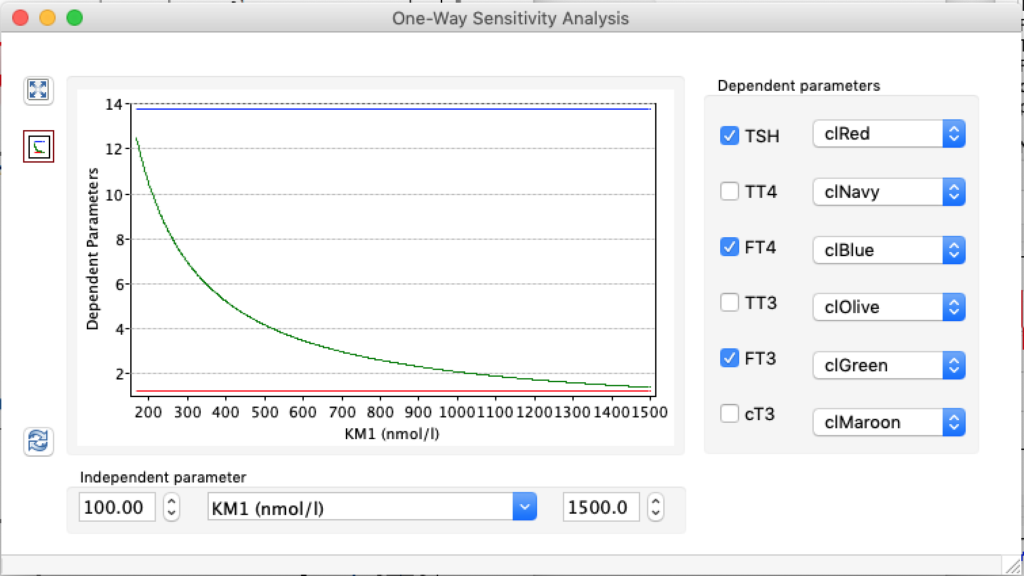
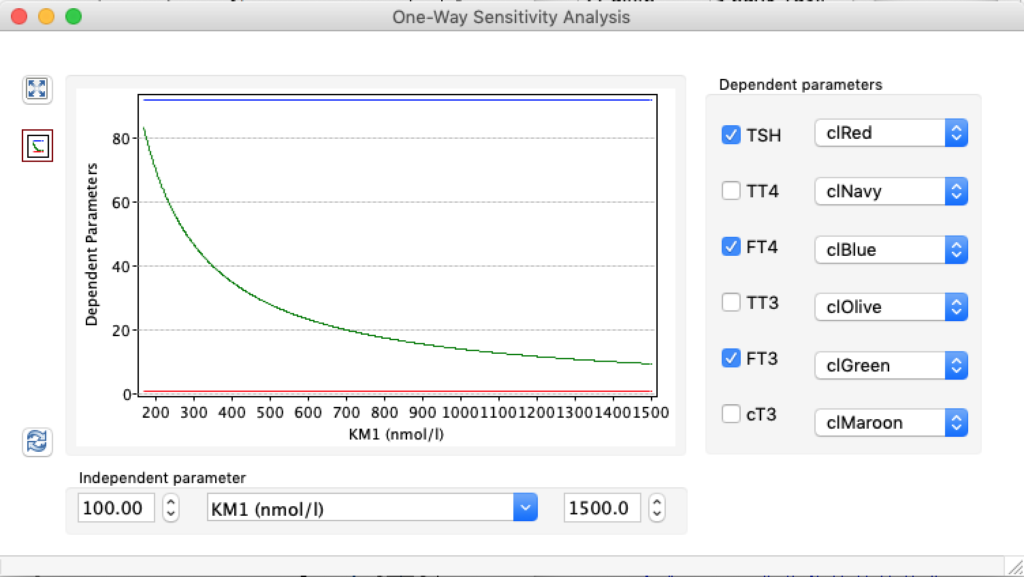
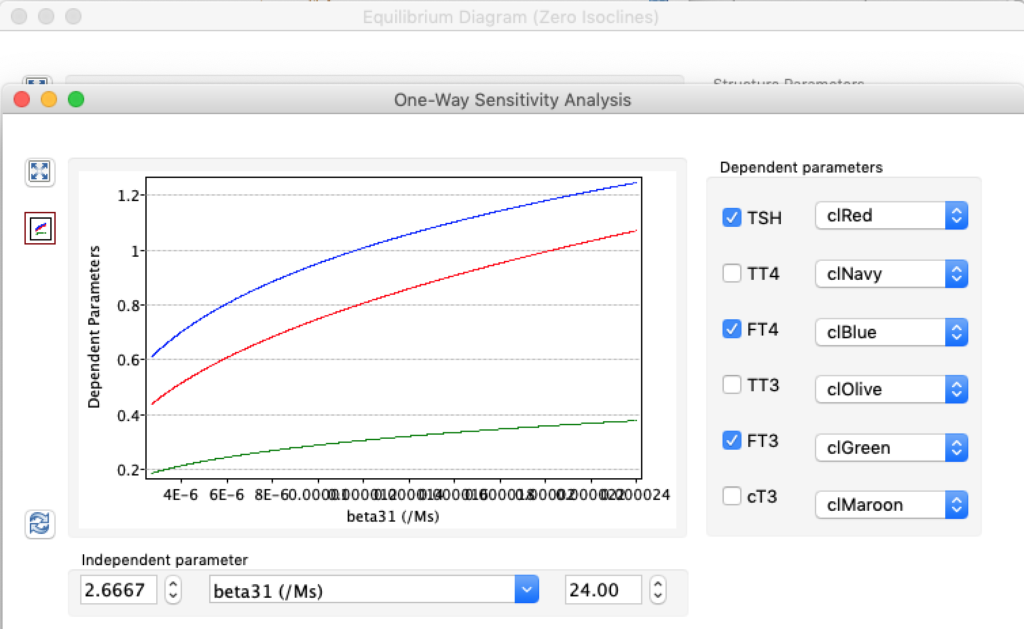
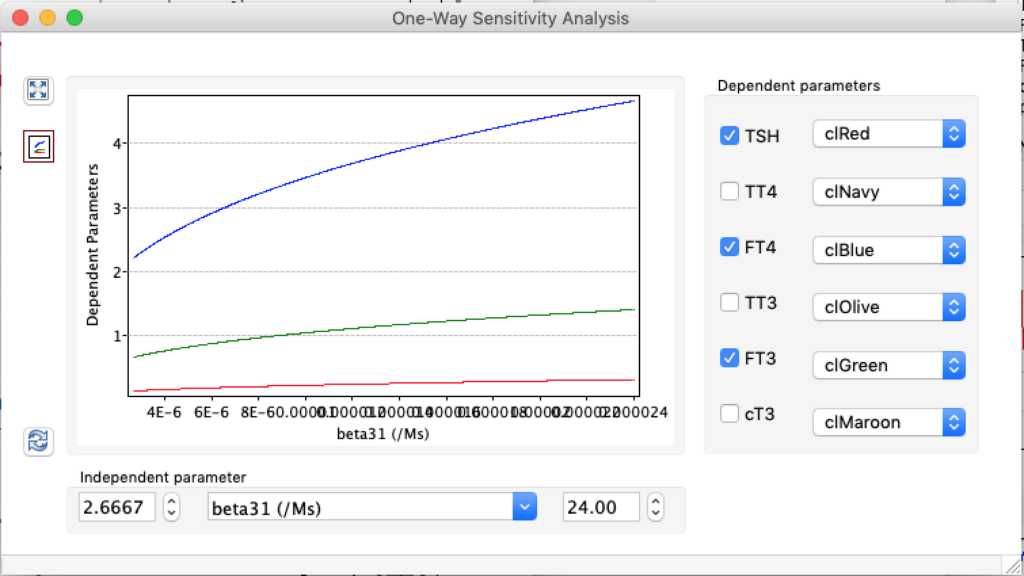
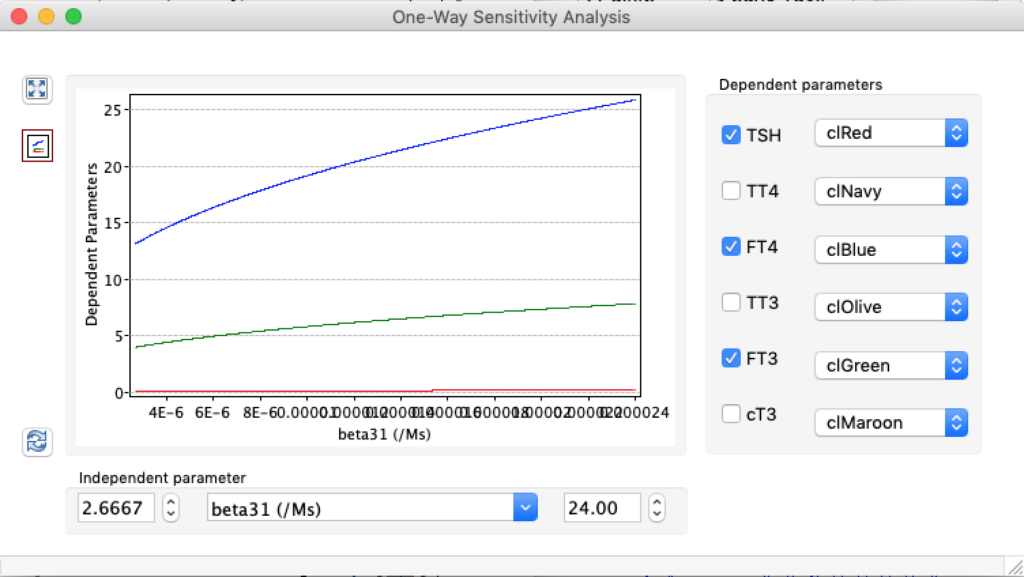
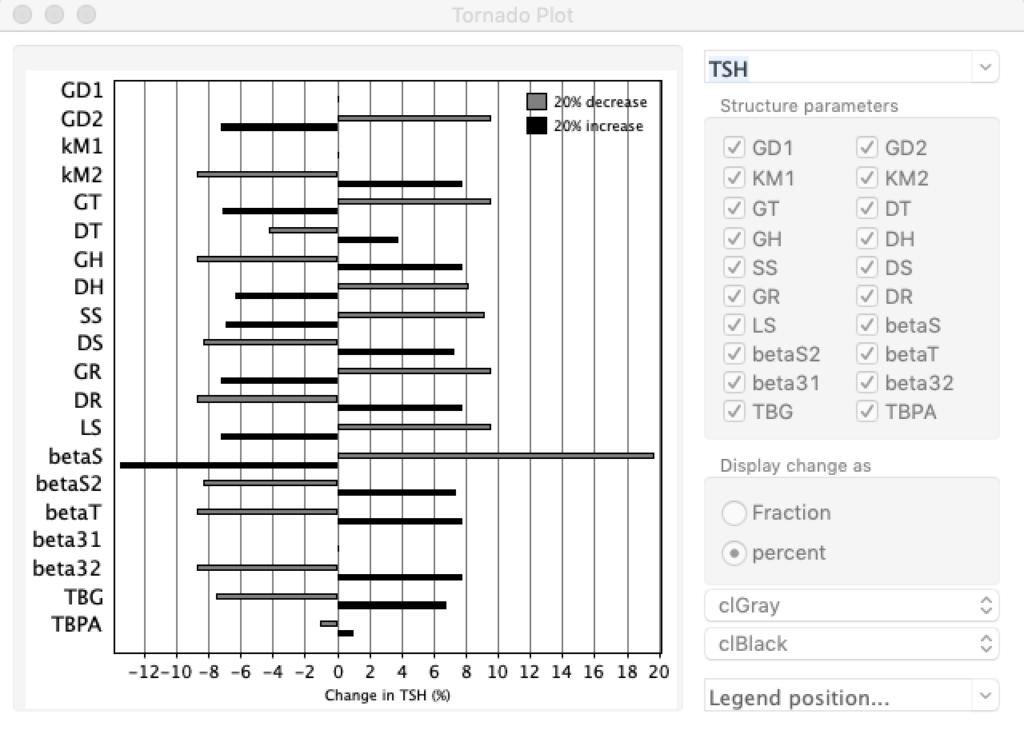
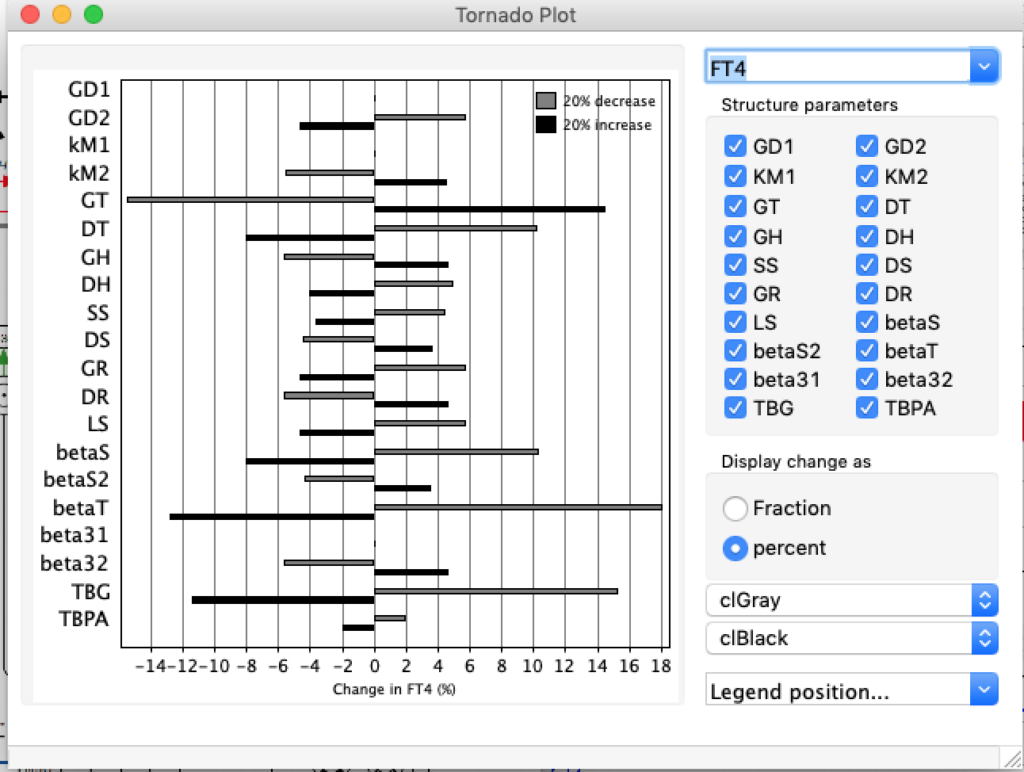
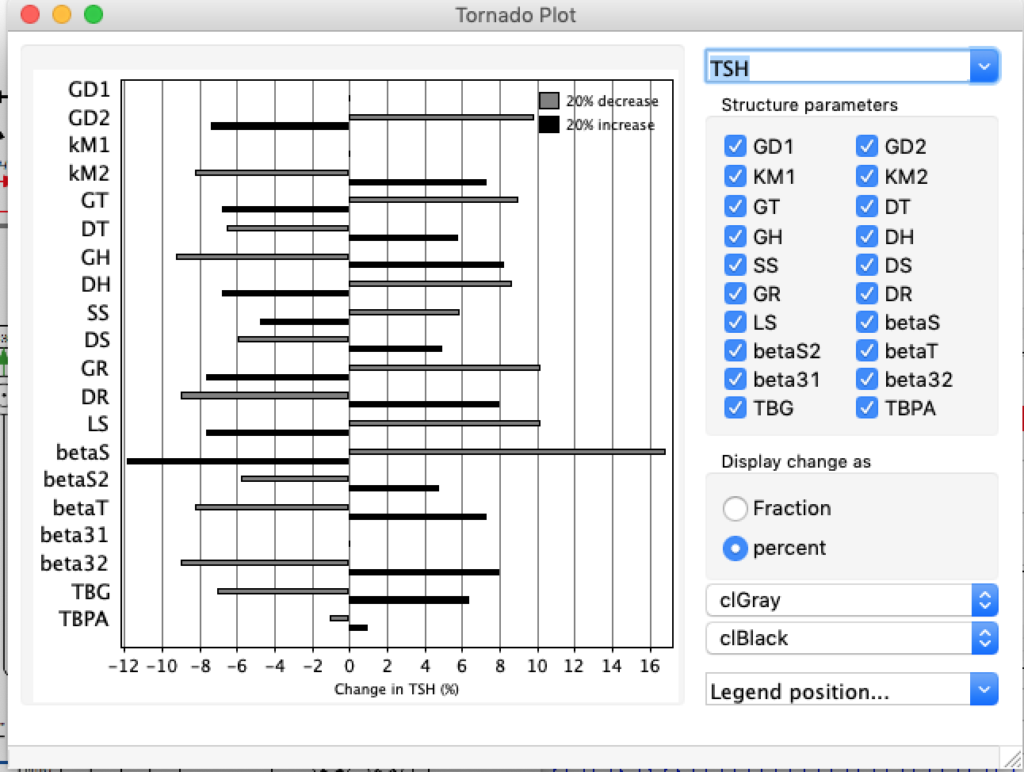
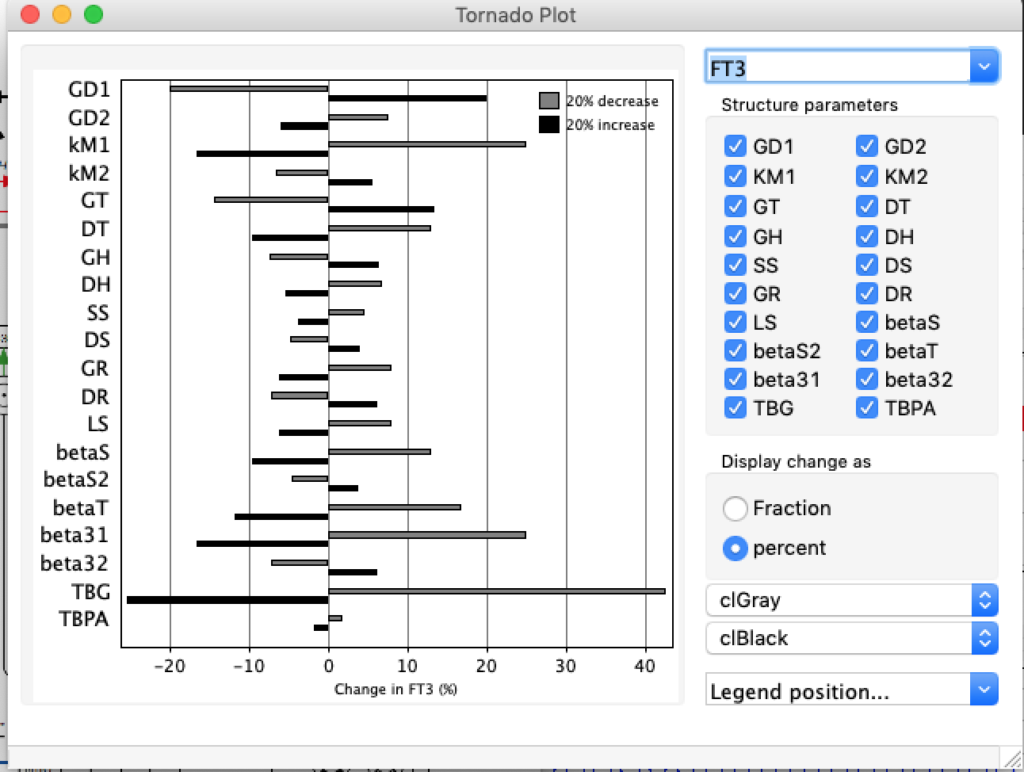
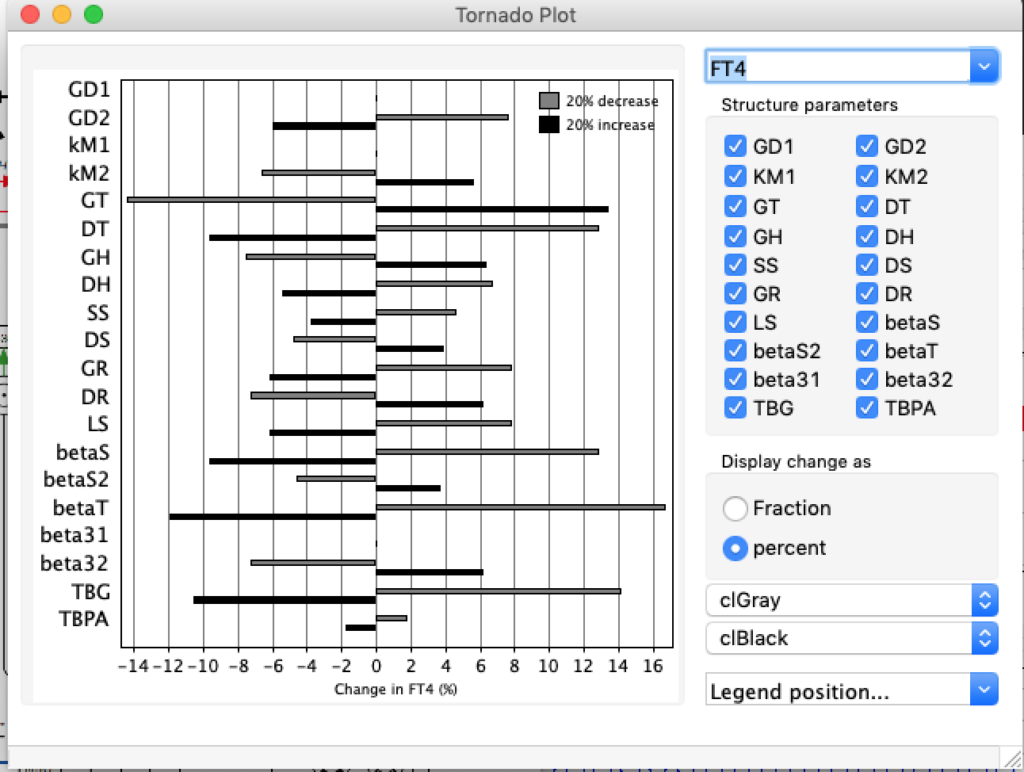
LS: Brake constant of feedback path #1 (Astwood-Hoskins loop)

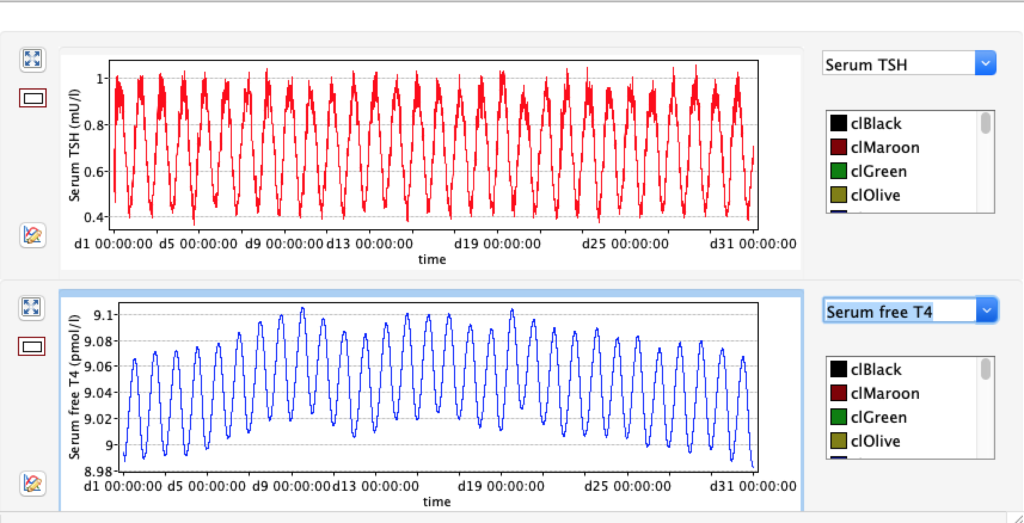
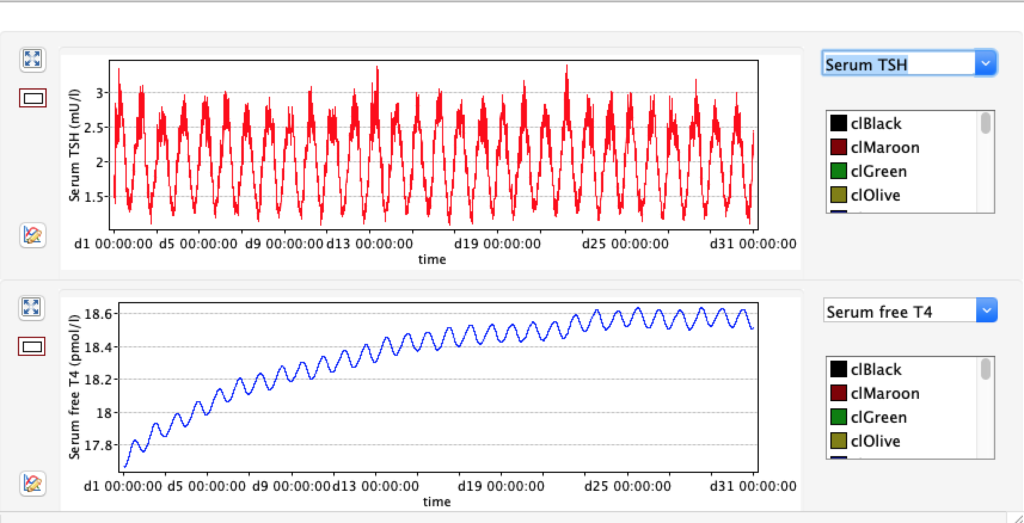
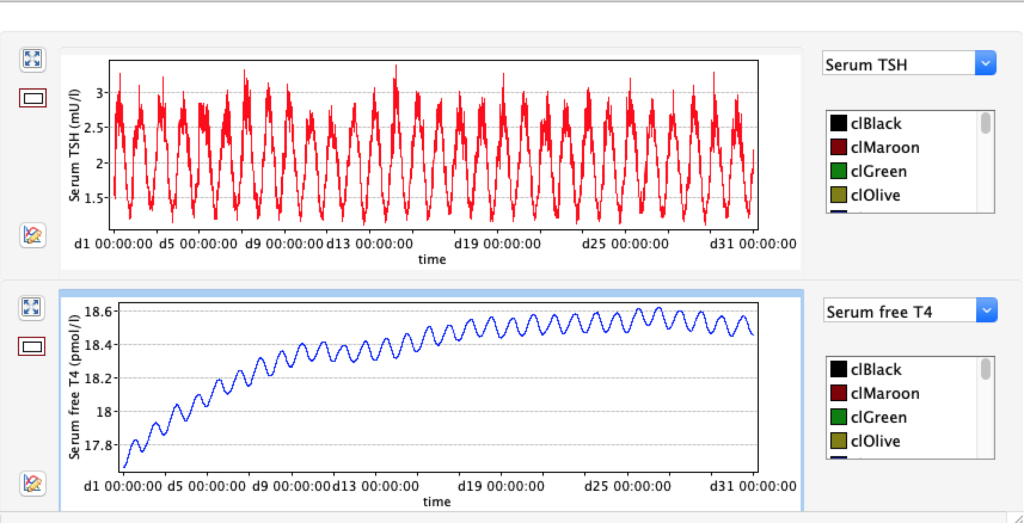
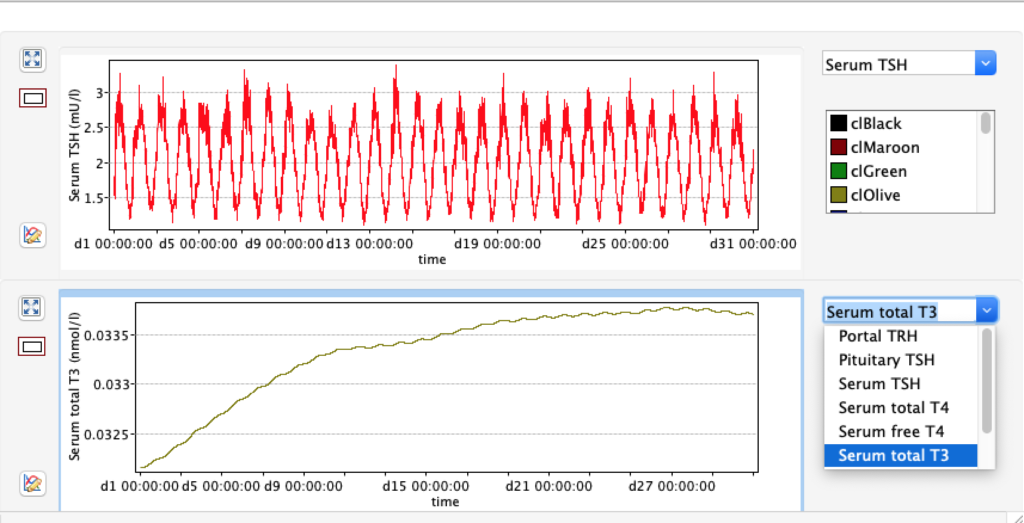
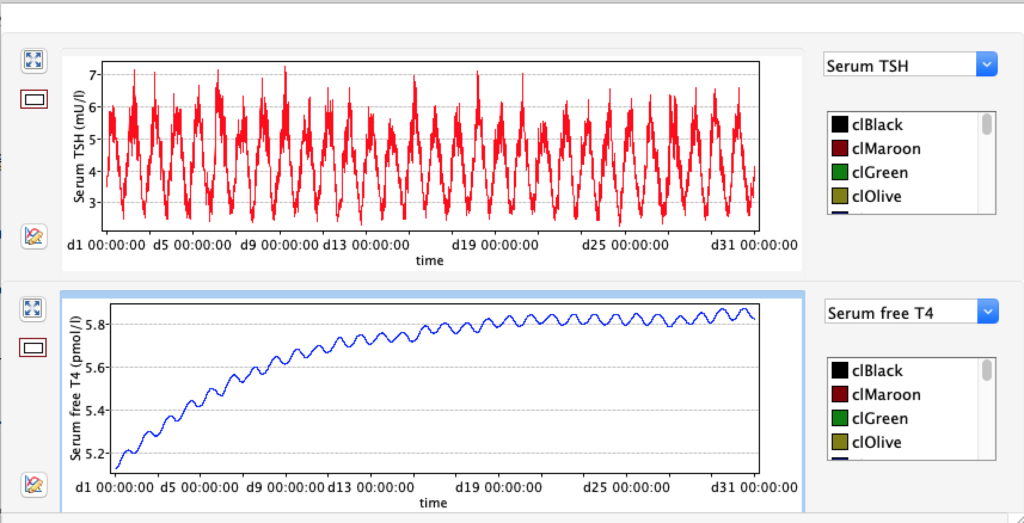
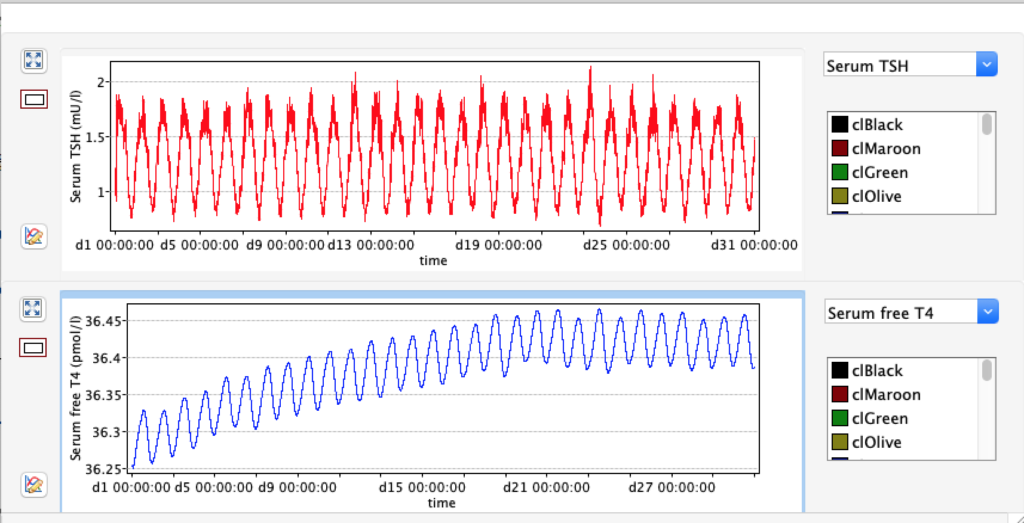
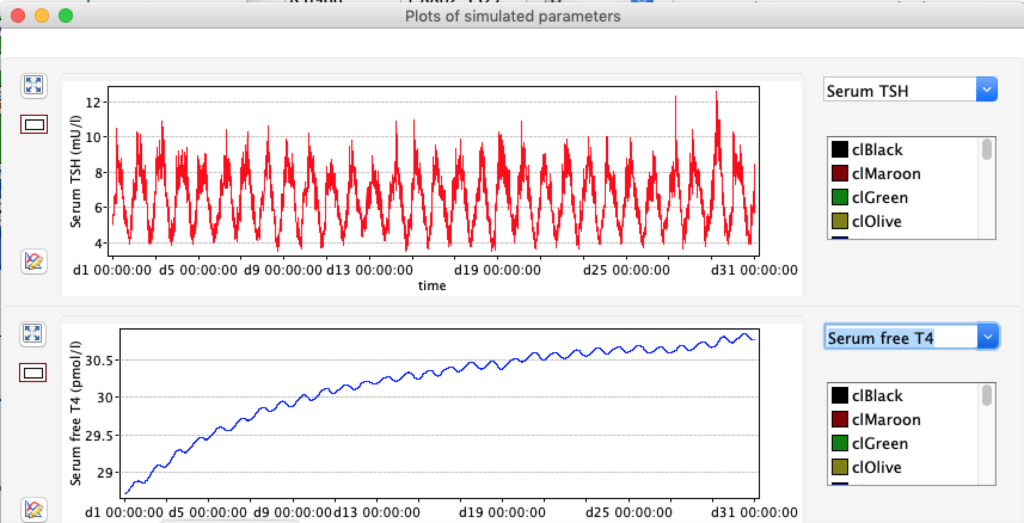
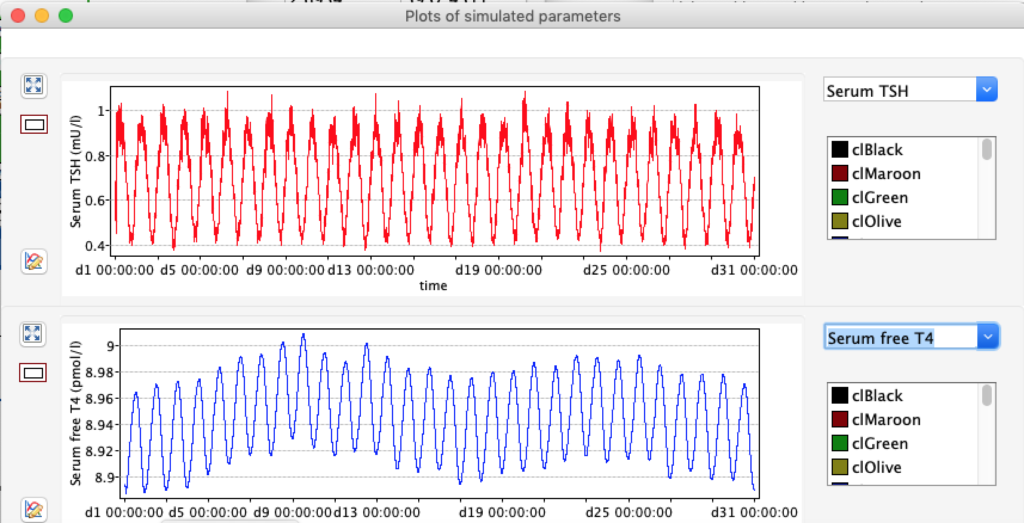
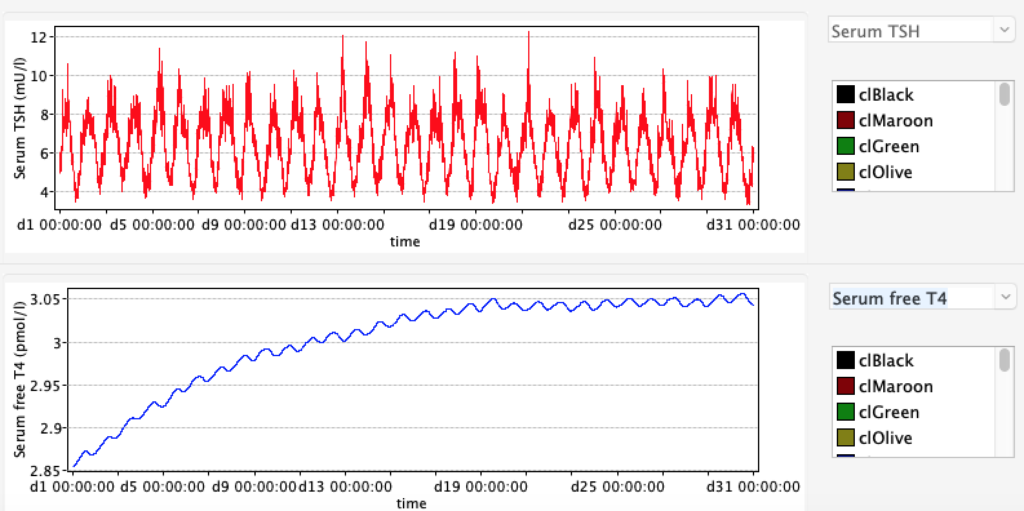
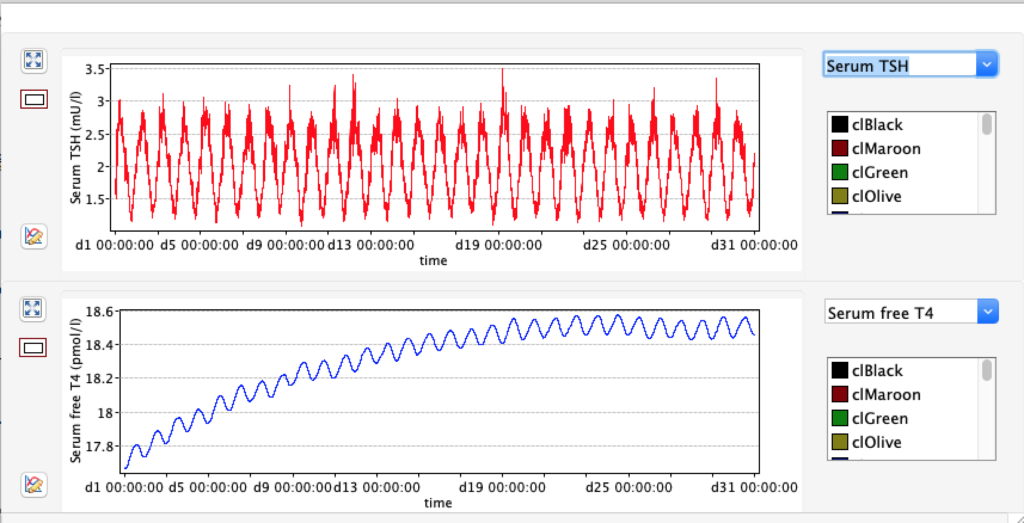
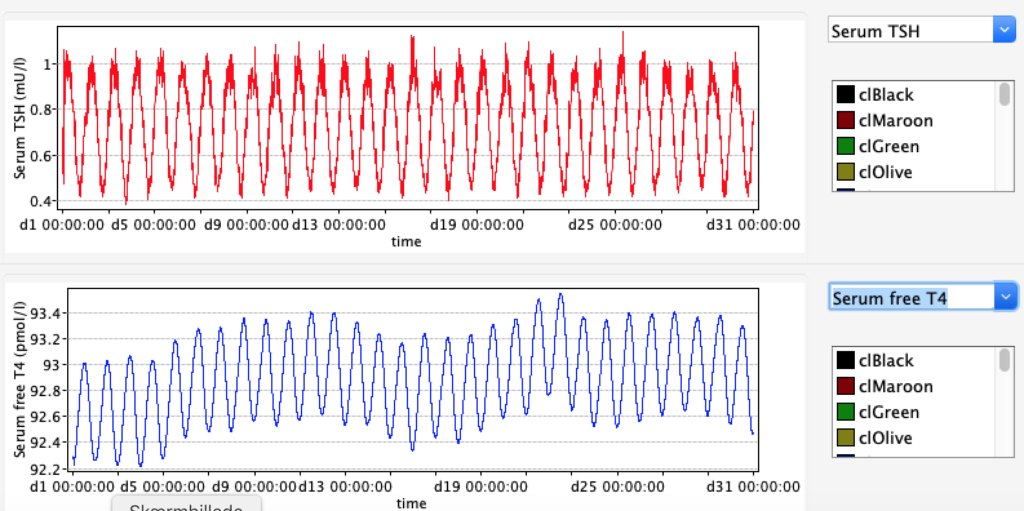
The damping constant of LS located in the pituitary is about 1,08 ± 0,14 l/µmol for the total group and in the untreated group (where hypothyroidism belongs) the figures are 1,78 ± 0,27 l/µmol.

Damping is an influence within or upon an oscillatory system that has the effect of reducing, restricting or preventing its oscillations. In physical systems, damping is produced by processes that dissipate the energy stored in the oscillation.

((https://www.miniphysics.com/natural-frequency.html))

TABLE 6. Decrease LS ( /10) STANDARD FIGURES Increase LS (x10)
TRH 2500 2500 2500
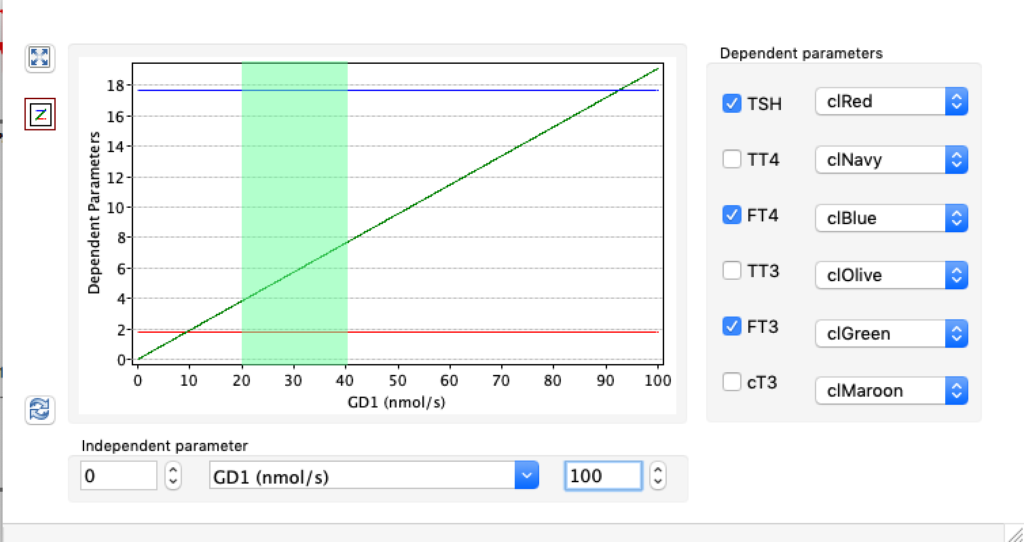
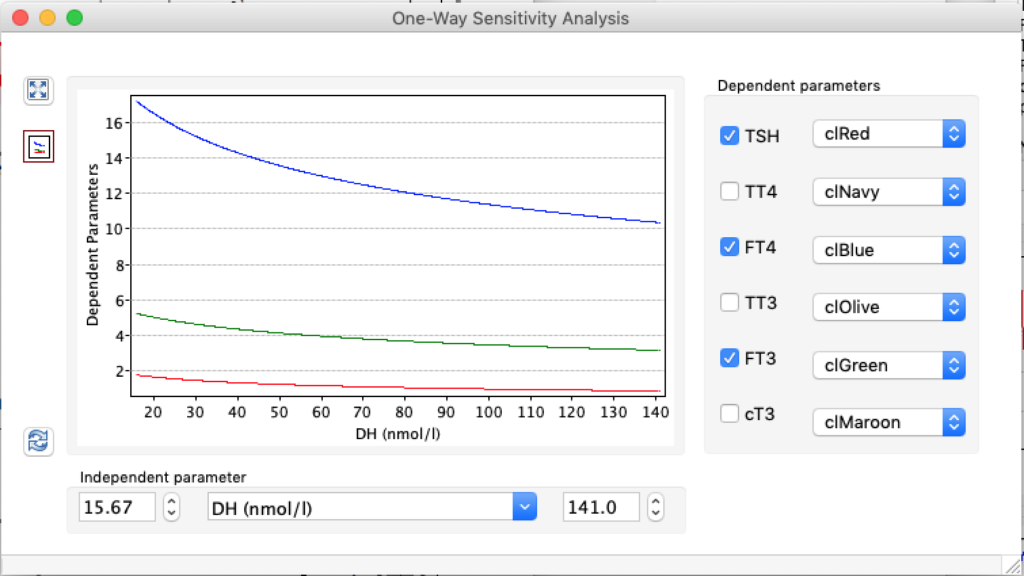
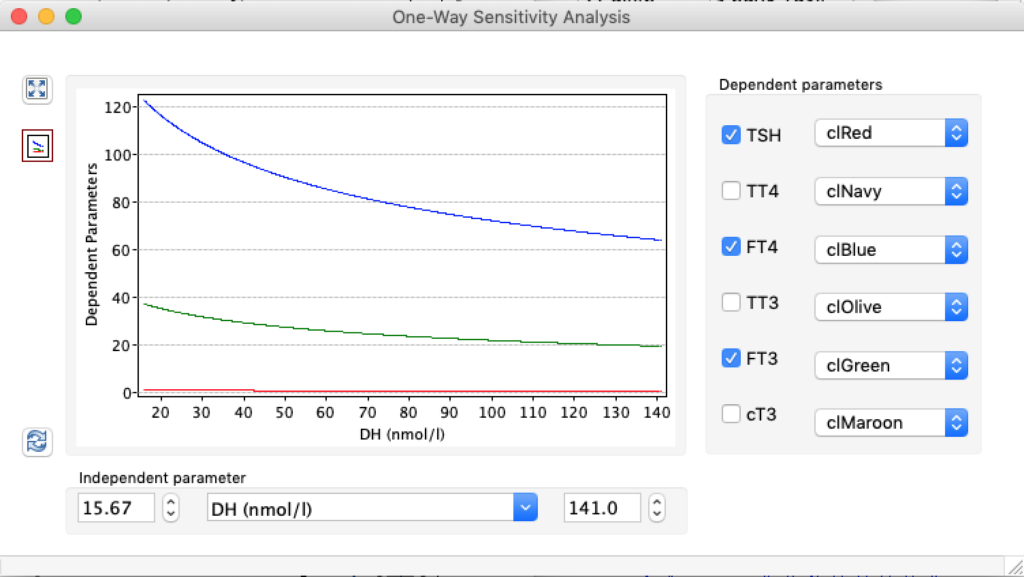
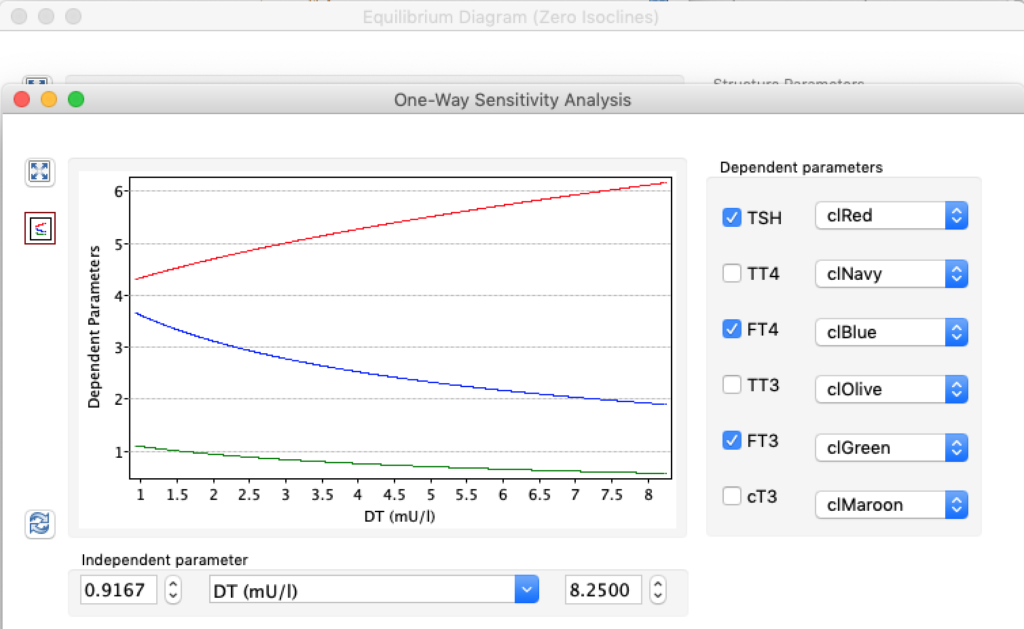
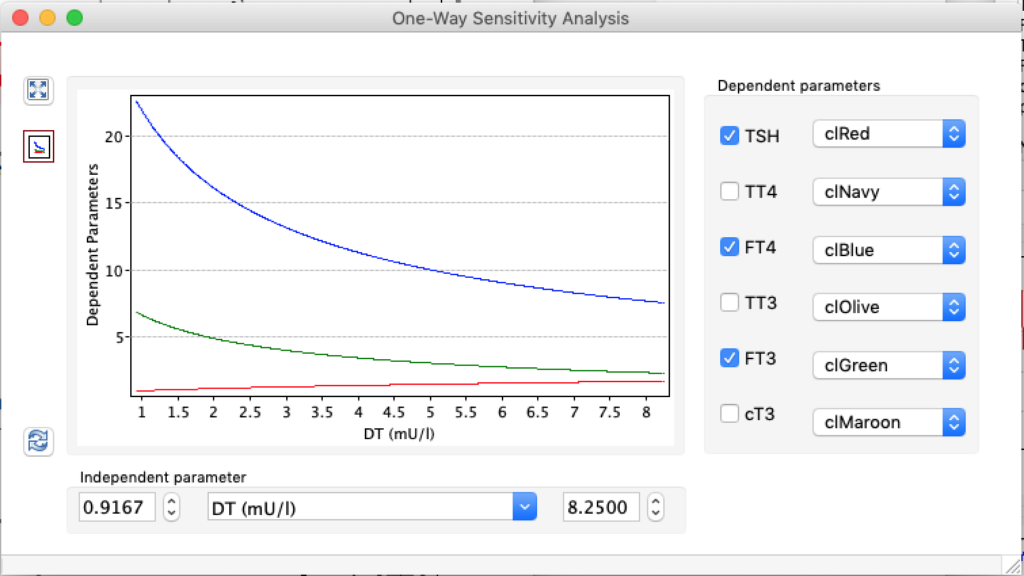
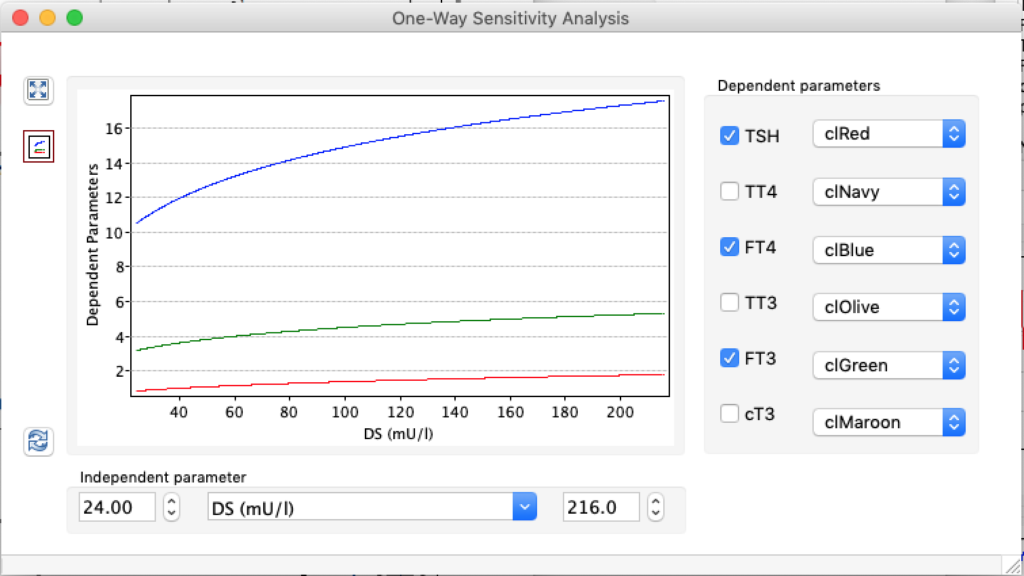
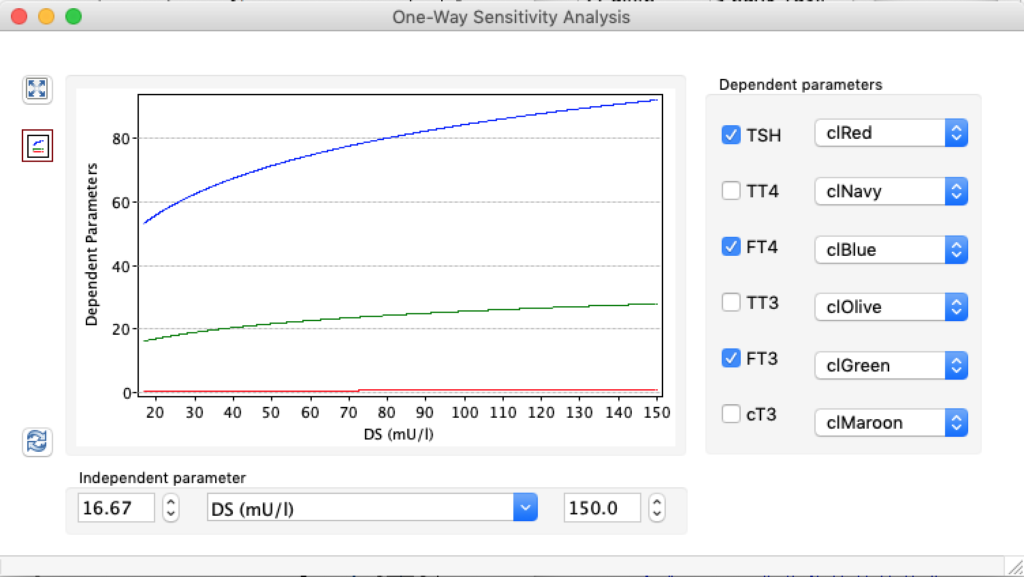
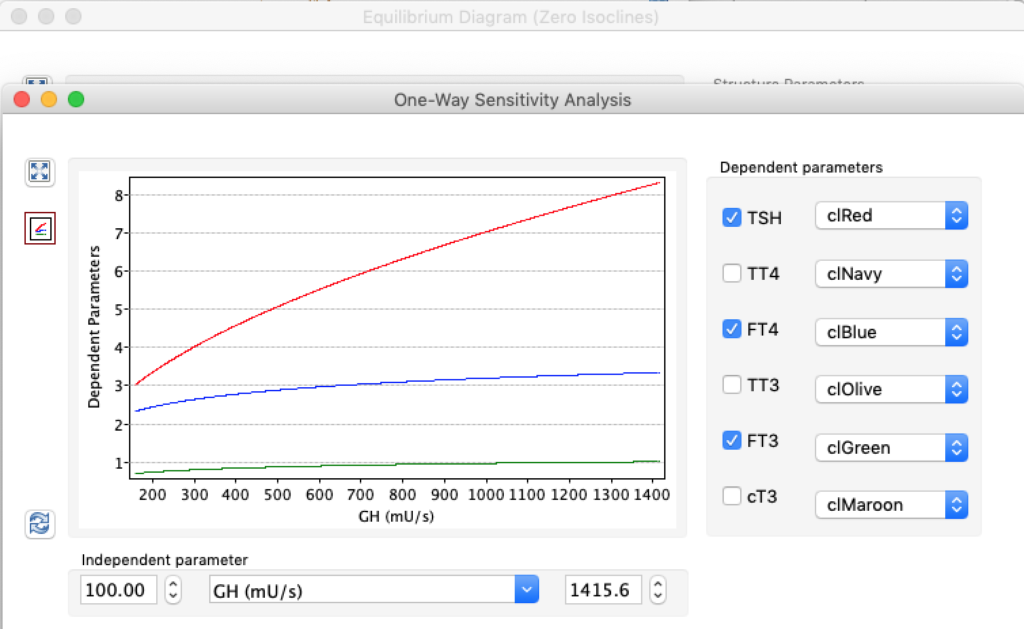
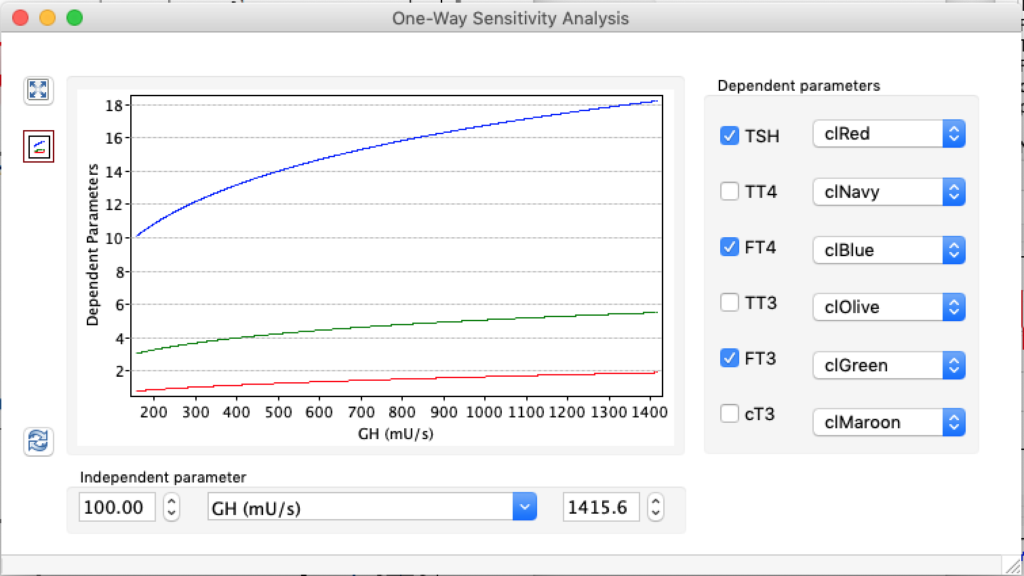
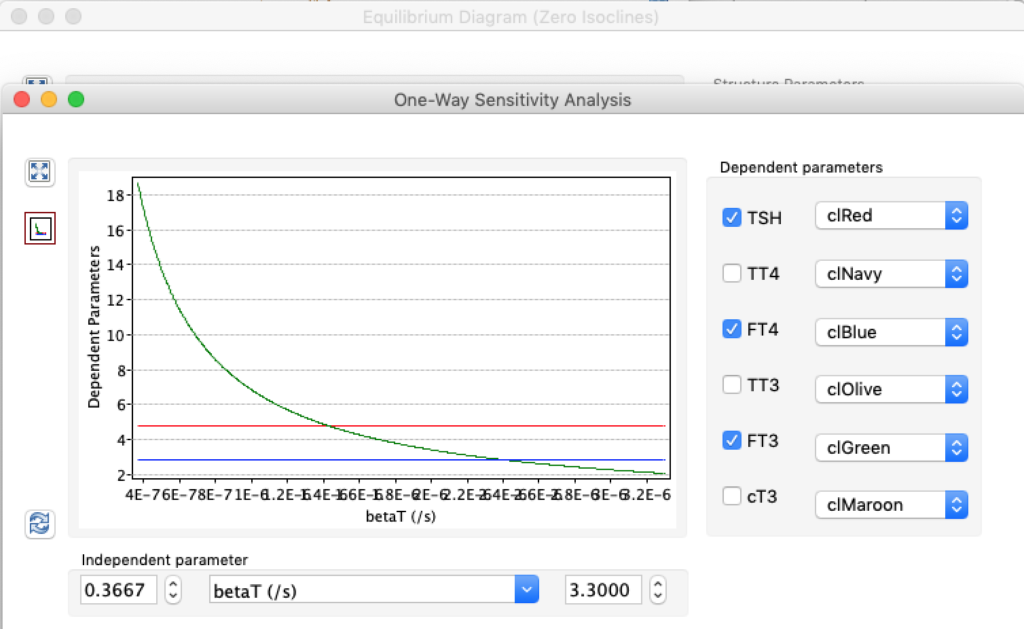
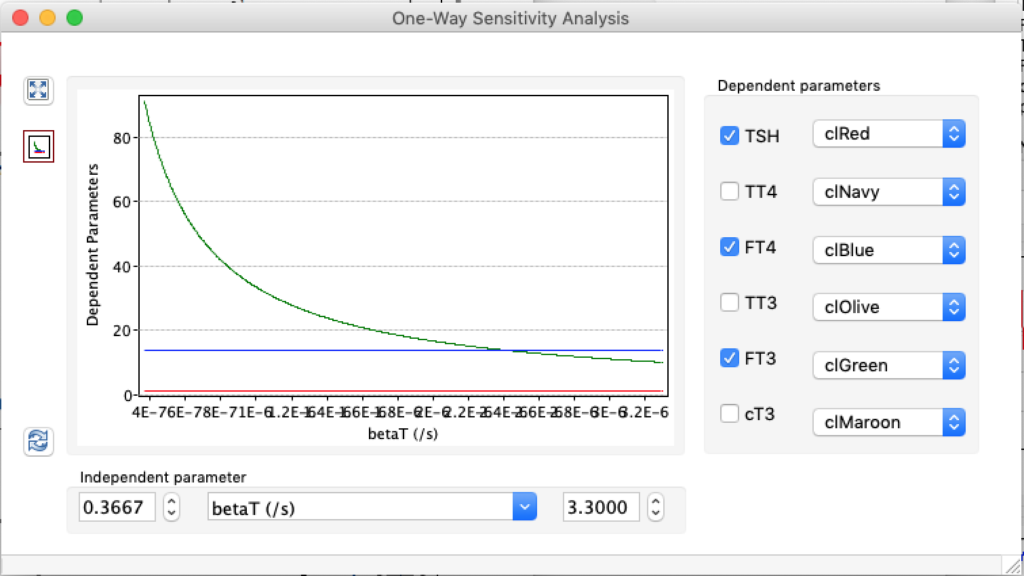
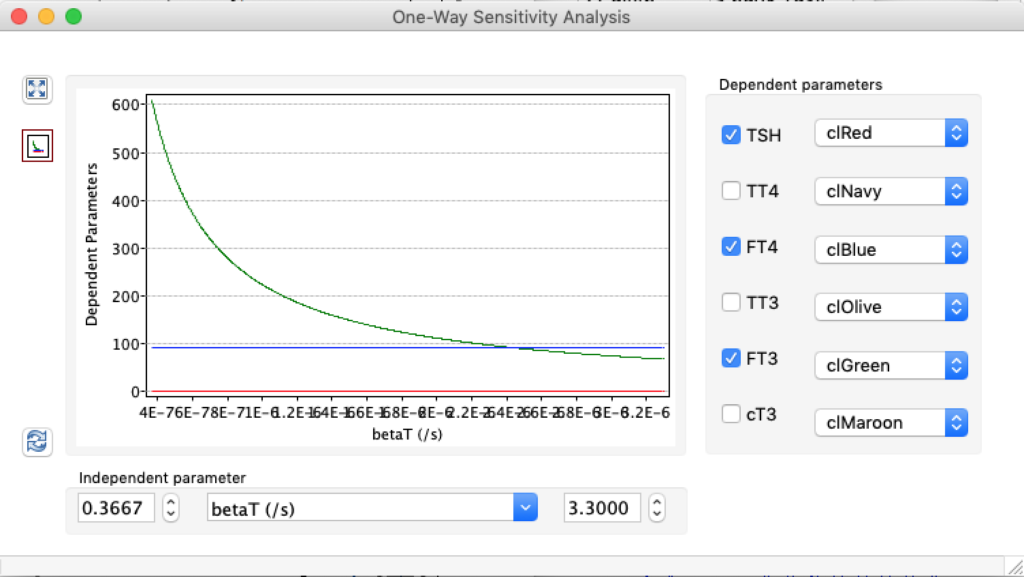
TSH 5,0166 1,8 0,6878
TT4 198,1796 121,94 61,3824
FT4 28,7175 17,67 8,8947
TT3 5,2263 3,21 1,6188
FT3 8,696 5,35 2,6935
cT3 18801,1569 11693,7490 5937,7172
LS – Reduced ten times
LS – Standard figures
LS – increased ten times

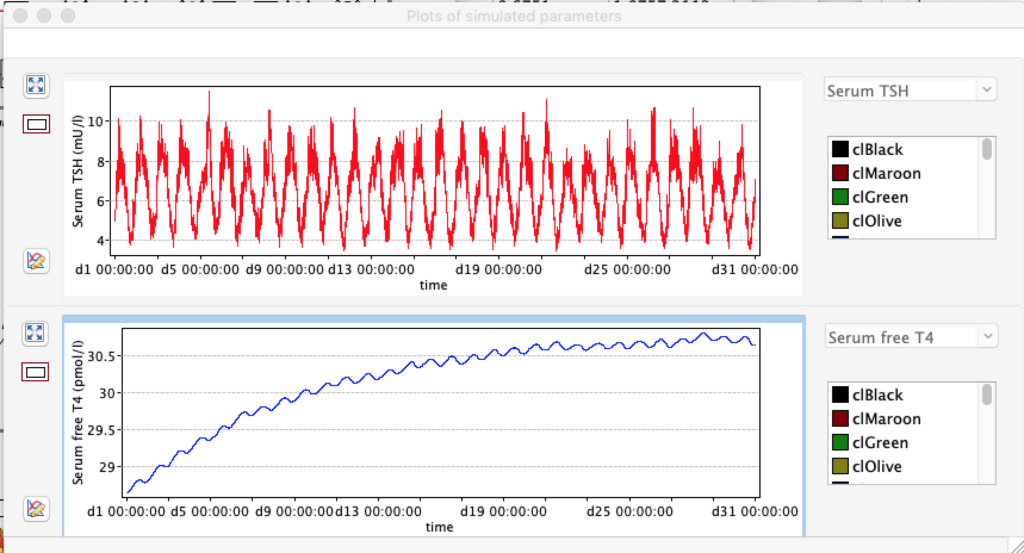
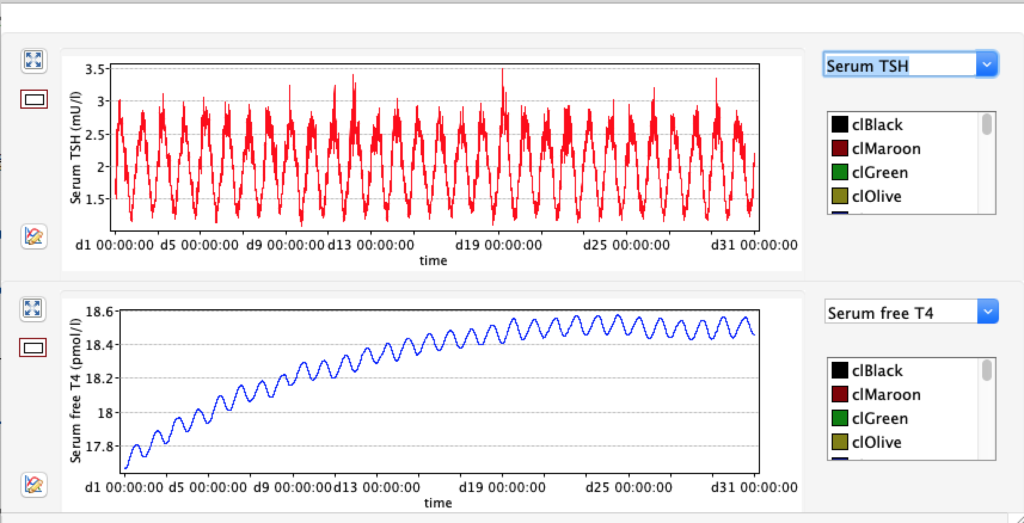
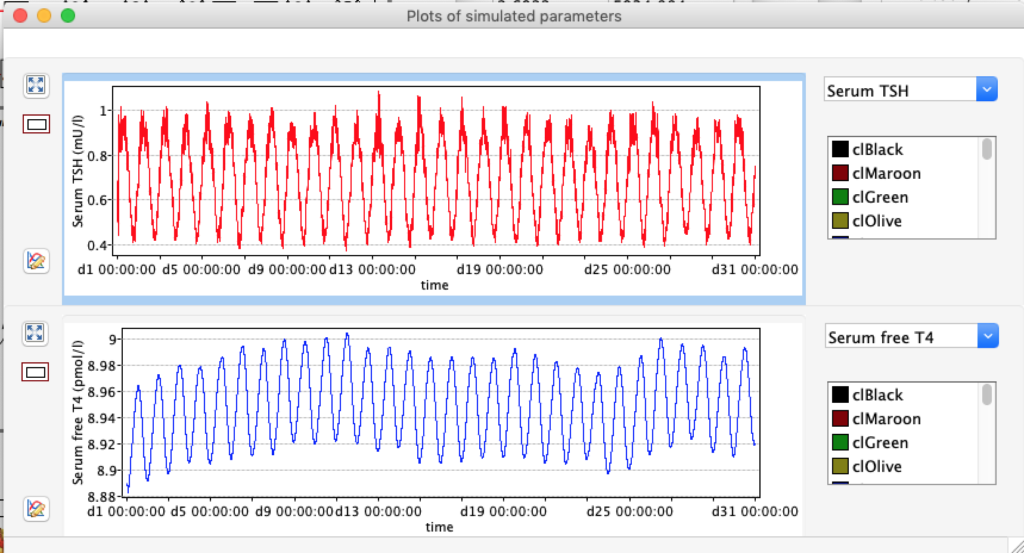
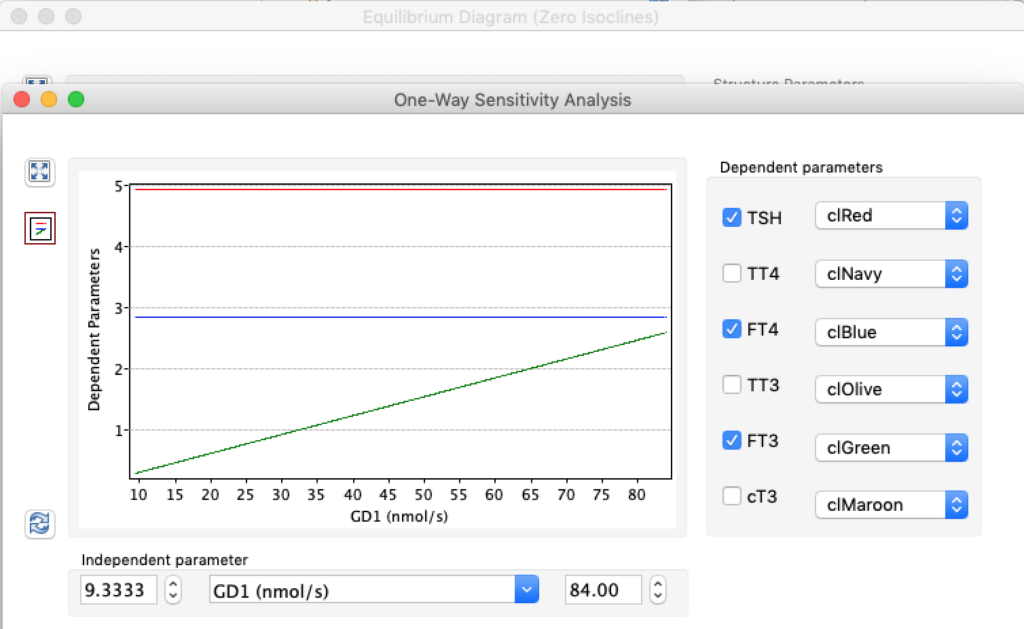
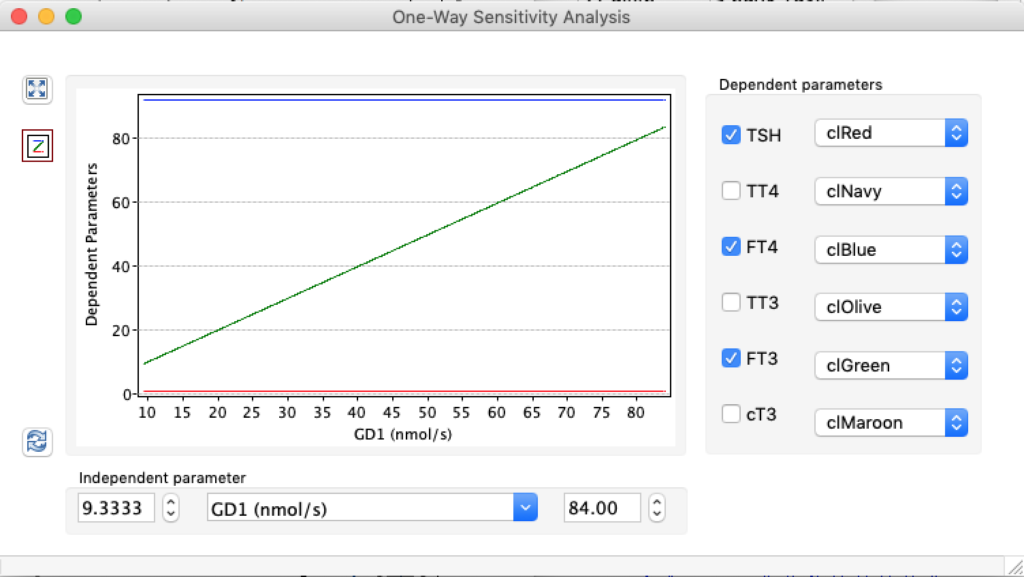
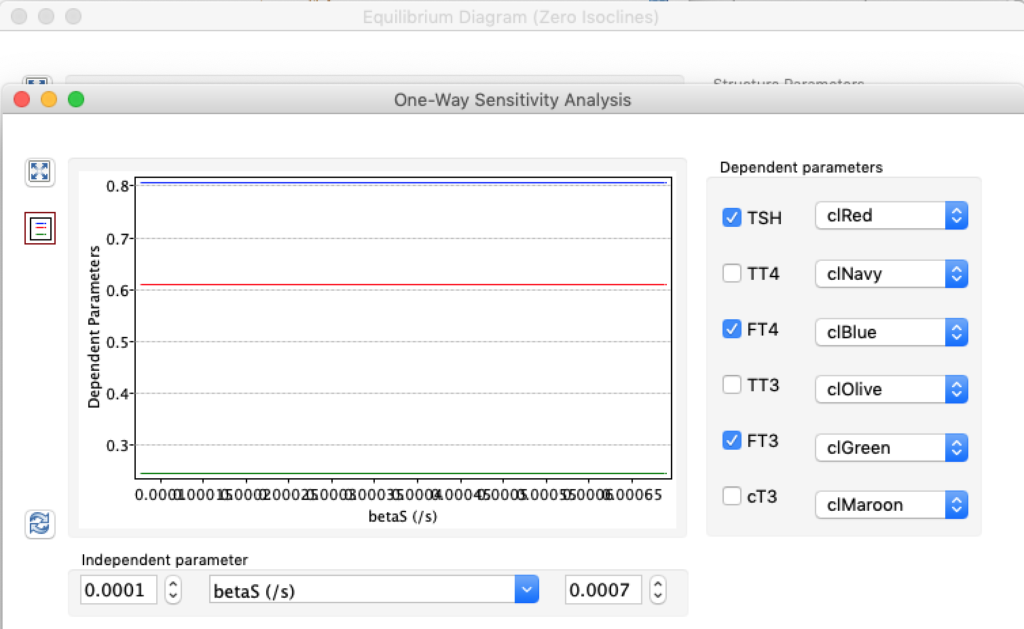
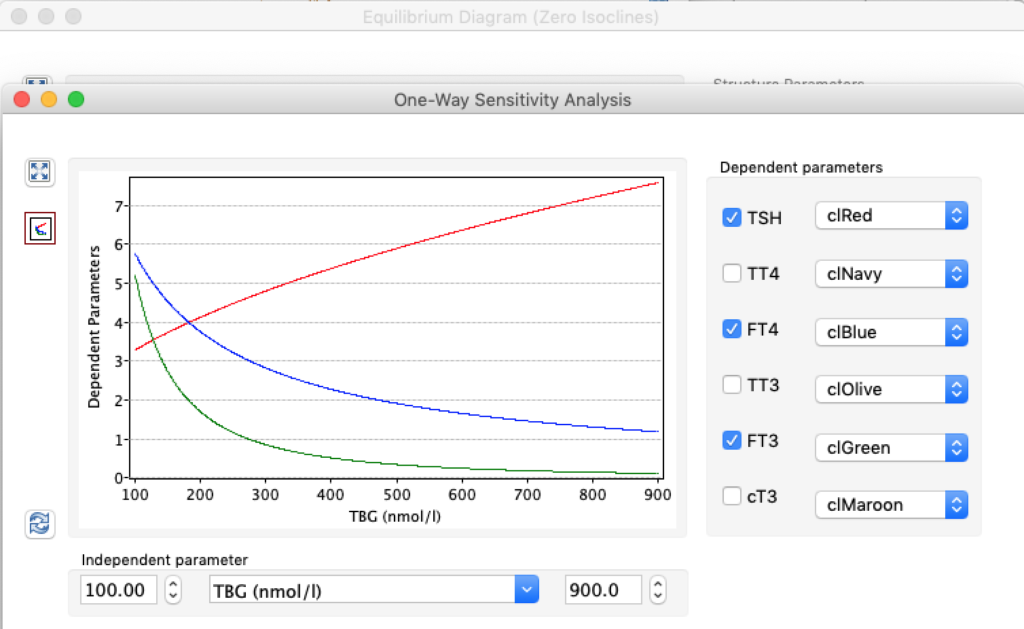
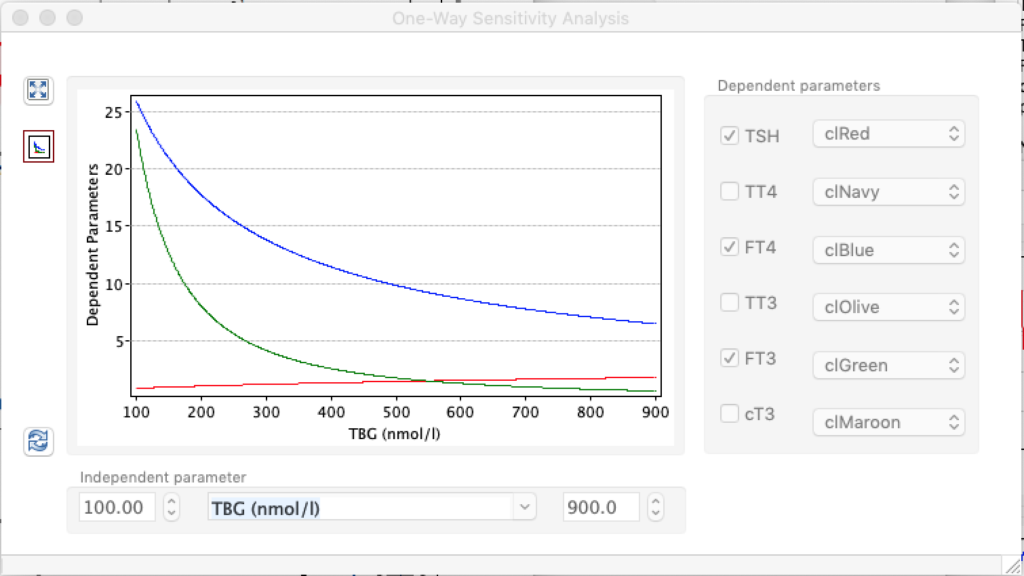
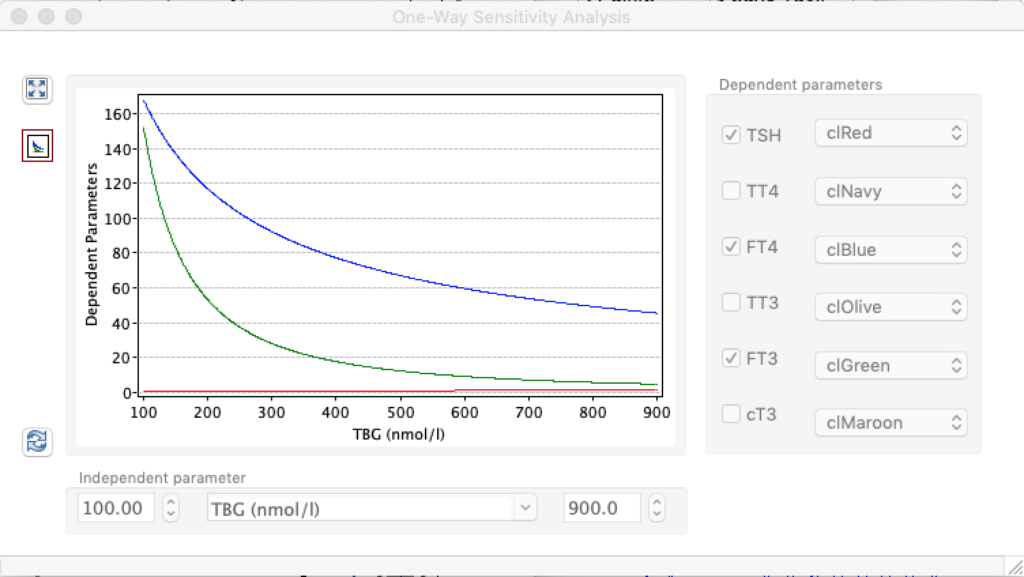
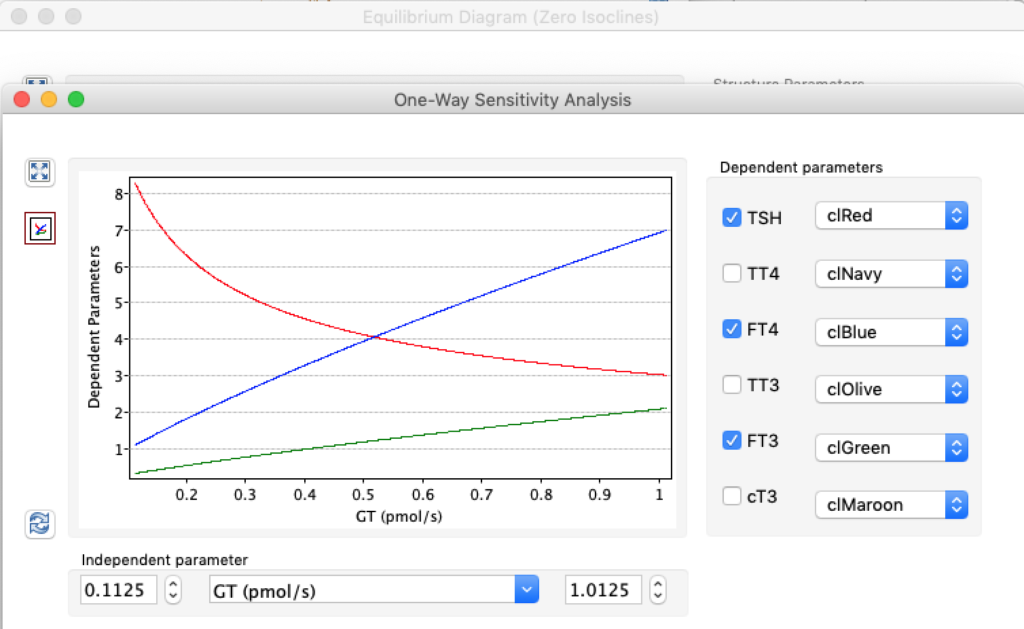
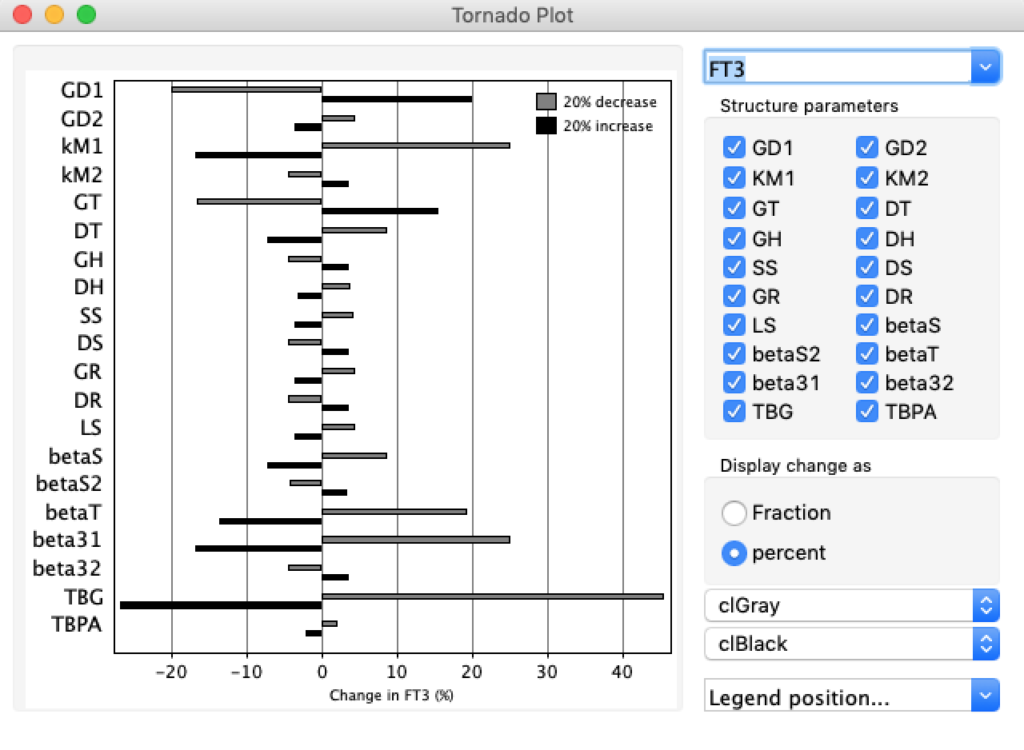
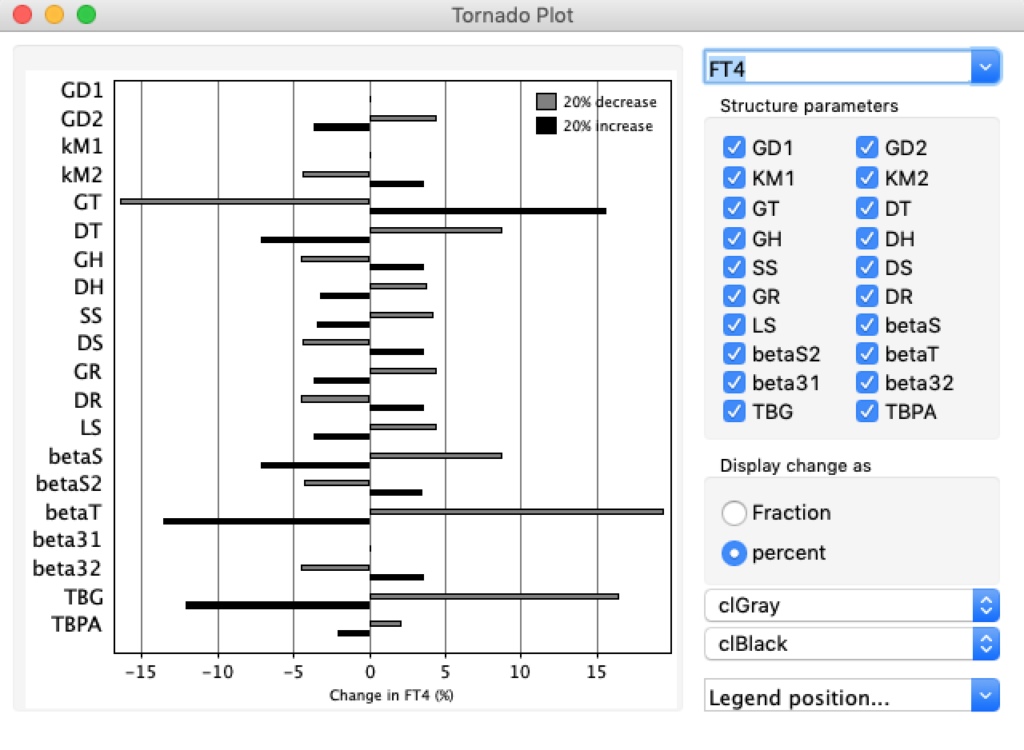
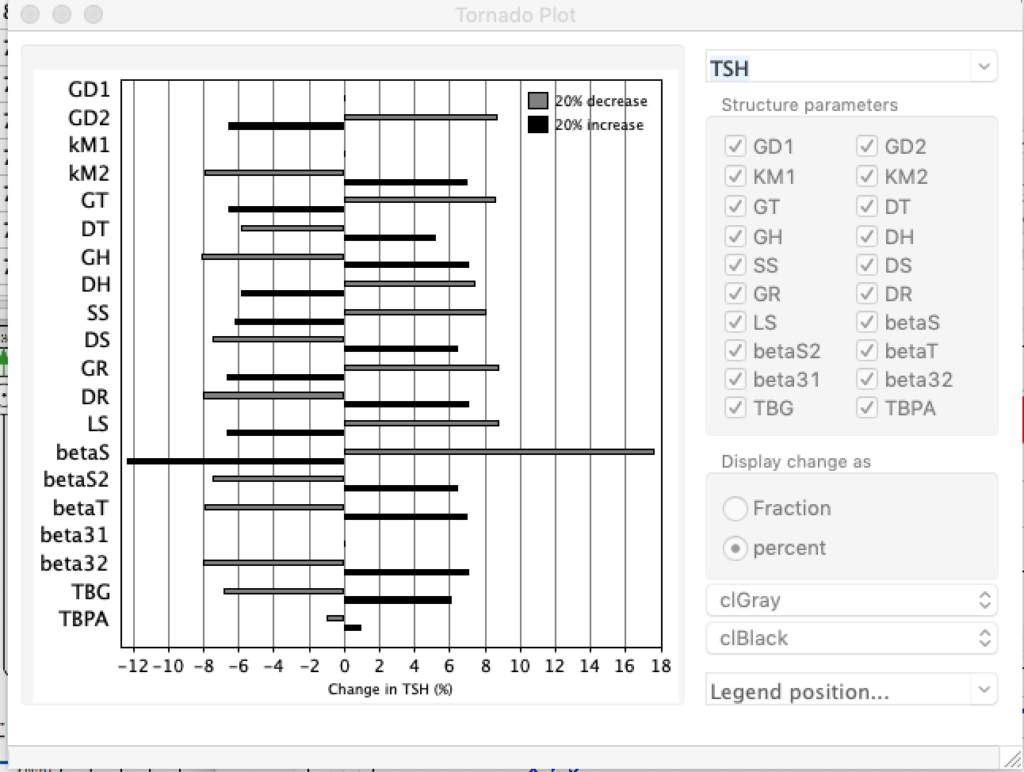
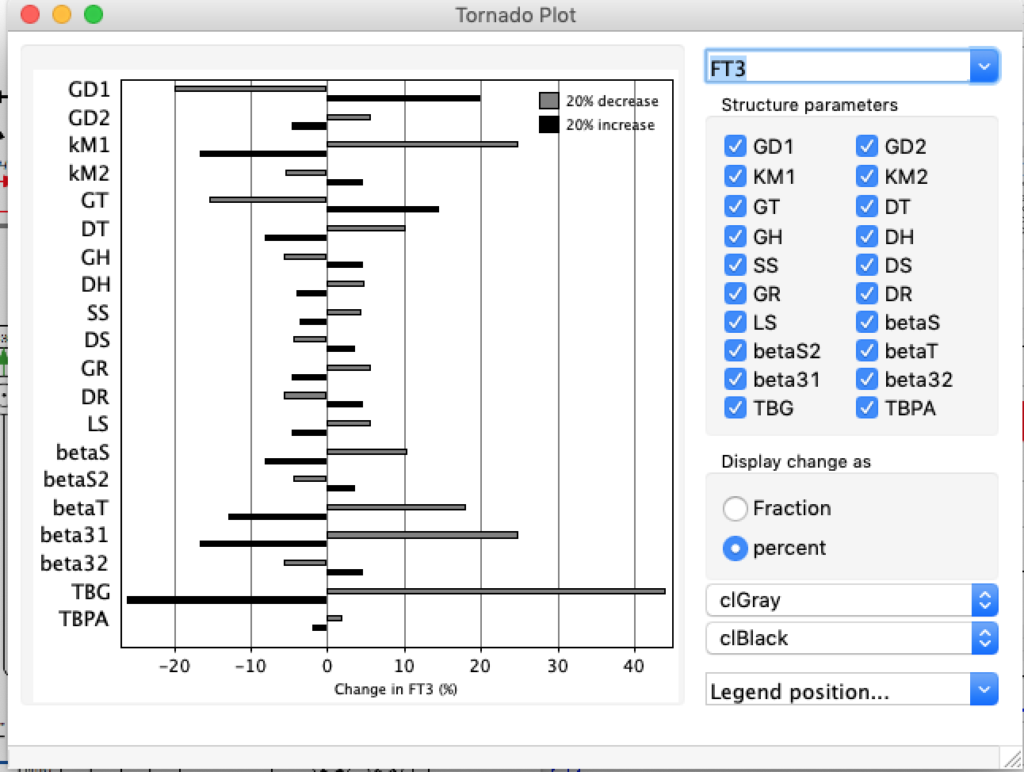
When keeping all other parameters constant, the damping constant of the main regulatory loop (LS) was found to differ significantly in the hypothyroid, euthyroid or hyperthyroid ranges (table 1). Similar to the gradients in the log TSH-FT4 relation, dampening constants (LS) differed in the different thyroid function states. Sensitivity analysis could, at least partly, explain the observed differences on the basis of distinct regulatory patterns that are operative under different conditions.
Hence, Hoermann et al propose a hierarchical type of control (see The Circle) exerted by a multimodal process with several controllers (shown in Simthyr as Constant Structures Parameters) and separate operating ranges of each controller. (See: Supplemental Material in Berberich J, Dietrich JW, Hoermann R and Müller MA (2018) Mathematical Modeling of the Pituitary–Thyroid Feedback Loop: Role of a TSH-T3 -Shunt and Sensitivity Analysis. Front. Endocrinol. 9:91. doi: 10.3389/fendo.2018.00091

Thus, the classical FT4-TSH feedback regulation represented by the parameters GT, GR, DR and LS appears to be more actively involved in TSH regulation in the hyperthyroid state,

.

KM 2

Af

KM 2: dissociation constant of type 2 deiodinase

TABLE 8.1 Decrease KM 2 ( /10 ) 1E-10 STANDARD FIGURES Increase KM 2 (x10) 1E-8
TRH 2500 2500 2500
TSH 0.7204 1,8 4.9344
TT4 63.6932 121,94 197.0175
FT4 9.2296 17,67 28.5491
TT3 1.6798 3,21 5.1956
FT3 2.7949 5,35 8.6450
cT3 56908.1934 11693,7490 1917.2921
KM 2 increase
basis
Standard values
KM 2 decrease

Explain dissociation constants: In chemistry, biochemistry, and pharmacology, a dissociation constant () is a specific type of equilibrium constant that measures the propensity of a larger object to separate (dissociate) reversibly into smaller components, as when a complex falls apart into its component molecules, or when a salt splits up into its component ions. The dissociation constant is the inverse of the association constant. In the special case of salts, the dissociation constant can also be called an ionization constant

GD 2

Af

GD 2: Sum activity of central type 2 deiodinase (D2)

TABLE 8. Decrease GD2 ( /10 ) 4.3E-16 STANDARD FIGURES Increase GD2 (x10) 4.3E-14
TRH 2500 2500 2500
TSH 4.9923 1,8 0.6974
TT4 197.8387 121,94 62.0698
FT4 28.6681 17,67 8.9943
TT3 5.2173 3,21 1.6369
FT3 8.6810 5,35 2.7237
cT3 11693.7408 11693,7490 11693.7408

Changes in this parameter affects not only the T3 values but also TSH and the T4 values. Simulated values shown here:

basis

KM 1

Af

KM 1 – dissociation constant of type 1 deiodinase

Explain dissociation constants: In chemistry, biochemistry, and pharmacology, a dissociation constant () is a specific type of equilibrium constant that measures the propensity of a larger object to separate (dissociate) reversibly into smaller components, as when a complex falls apart into its component molecules, or when a salt splits up into its component ions. The dissociation constant is the inverse of the association constant. In the special case of salts, the dissociation constant can also be called an ionization constant.

TABLE 7.1 Decrease KM1 ( /10 ) STANDARD FIGURES Increase KM1 (x10) 5E-6
TRH 2500 2500 2500
TSH 1.8138 1,8 1.8138
TT4 121.9379 121,94 121.9379
FT4 17.6696 17,67 17.6696
TT3 32.1473 3,21 0.3216
FT3 53.4897 5,35 0.5351
cT3 11693.7408 11693,7490 11693.7408
basis
Standard values

No changes in the TSH, T4 or free T4 values but marked changes in the T3 and free T3 values:

Increase and decrease of KM 1 has the opposite effect of GD 1.

GD 1

Af

GD 1: Sum activity of peripheral type 1 deiodinase (D1)

TABLE 7. Decrease GD1 ( /10 ) STANDARD FIGURES Increase GD1 (x10) 2.8E-7
TRH 2500 2500 2500
TSH 1.8138 1,8 1.8138
TT4 121.9379 121,94 121.9379
FT4 17.6696 17,67 17.6696
TT3 0.3216 3,21 32.1575
FT3 0.5351 5,35 53.5067
cT3 11693.7408 11693,7490 11693.7408

When the sum activity of deiodinase increases we only see changes in the T3 an fT3 parameters.

basis
No remarkable changes between these two scenarios
Standard values
fT3 values increased 10 times – without any influence at TSH/fT4

DT

Af

DT: Damping constant (EC50) of TSH at the Thyroid.

TABLE 11 Decrease DT ( /10 ) STANDARD FIGURES Increase DT (x10)
TRH 2500 2500 2500
TSH 1.2151 1,8 3.5831
TT4 250.1930 121,94 35.3682
FT4 36.2546 17,67 5.1251
TT3 6.5979 3,21 0.9328
FT3 10.9781 5,35 1.5520
cT3 23562.9892 11693,7490 3434.1110

When the dampening constant is increased we see these changes in the thyroid hormones. Visualised below:

The standard figures visualised:

basis

When the dampening constant is decreased we see these changes in the thyroid hormones. Visualised below:

decreased DR

GH

Af

The pituitary receives information TRH from the hypothalamus and sends information TSH to the thyroid depending on the state of T4 and T3 in the body.

GH: the secretory capacity of the pituitary

TABLE 2. Decrease GH (/10) STANDARD FIGURES Increase GH (*10)
TRH 2500 2500 2500
TSH 0,6877 1,8 5,0176
TT4 61,3794 121,94 198,1946
FT4 8,8943 17,67 28,7197
TT3 1,6187 3,21 5,2267
FT3 2,6934 5,35 8,6966
cT3 5937,4311
18802,5327

These are the standard curves:

Increased GH increased TSH/T4 and the opposite with the decreased values. It seems as if fT4 despite fluctuations falls slightly over the 30-day simulation

GT

Af

The thyroid secretes T4 and T3 – and GT is a central parameter in the SimThyr model.

GT has been observed to correlate with thyroid volume as determined by ultrasonography and to be elevated in hyperthyroidism and reduced in hypothyroidism [11, 116].
Recently, a small study that has been published as an abstract revealed calculating GT to be beneficial in differential diagnosis of NTIS with thyrotropic adaptation and latent (subclinical) hyperthyroidism.
This feedback loop might prevent excessively high TSH levels and also be a source of TSH pulsatility, as suggested by investigations based on fractal geometry [49].
The existence of this loop may be a challenge for interpretation of laboratory results, especially in patients with Graves’ disease, where TRAbs may suppress TSH secretion independently from current FT4 levels [50] resulting in TSH levels being lower than expected in relation to current FT4 levels.

GT: the secretory capacity of the thyroid

TABLE 1. Decrease GT (3.375E-13) STANDARD FIGURES Increase GT (3.375E-11)
TRH 2500 2500 2500
TSH 4,9344 1,8 0,7204
TT4 19,7017 121,94 636,9324
FT4 2,8549 17,67 92,2957
TT3 0,5196 3,21 16,7947
FT3 0,8645 5,35 27,9446
cT3 1917,2921
56908,1934

When the thyroid capacity is reduced we see changes in the thyroid hormones. Visualised below:

These are the standard curves:

When the thyroid capacity is increased we see changes in the thyroid hormones. Visualised below:

Patterns of developing hypothyroidism or hyperthyroidism.

One-Way Sensitivity Analysis – GT

Af

GD 1: Sum activity of peripheral type 1 deiodinase (D1).
As can be seen, TSH and fT4 are horizontal and fT3 levels increase with increased GD1 level. Reflecting that increase and decrease of GD1 only affects T3/fT3 values. The green area is the reference range for GD

GD1 Decreased
GD1 Increased
GD1 Decreased
GD Increased
BetaS Decreased
BetaS Standard
BetaS Increased
Beta S2 Decreased
Beta S2 Standard
Beta S2 Increased
TBG Decreased
TBG Standard
TBG Increased
TBPA Decreased
TBPA Standard
TBPA Increased
DH Decreased
DH Standard
DH Increased
DT Decreased
DT Standard

DT Increased
GD2 Decreased
GD2 Standard
GD2 Increased
GR Decreased
GR Standard
GR Increased
LS Decreased
LS Standard
LS Increased
SS Decreased
SS Standard
SS Increased
Beta31 Decreased
Beta31 Standard
Beta31 Increased
DR Decreased
DR Standard
DR Increased
DS Decreased
DS Standard
DS Increased
GH Decreased
GH Standard
GH Increased
KM2 Decreased
KM2 Standard
KM2 Increased
BetaT Decreased
BetaT Standard
BetaT Increased
GT Decreased
GT Standard
GT Increased
KM1 Decreased
KM1 Standard
KM1 Increased
Beta31 Decreased
Beta31 Standard
Beta31 Increased
Beta32 Decreased
Beta32 Standard
Beta32 Increased

HER

In the euthyroid state, others and we have observed a considerable interindividual variability in FT4, TSH and their regulatory set points.15 39 40

Diversity:
Possible molecular mechanisms may include either different individual concentrations and affinities of TRs, variations in the distribution of iodothyronine transporters or a polymorphism in the type 2 deiodinase, which in the presence of a homozygous allele weakens the negative feedback of FT4 on TSH in humans.40 41

Tornado plot – GT

Af

Decreased GT

3.375E-13 -TSH
3.375E-13 – FT3
3.375E-13 – FT4

Standard GT

Standard -TSH
Standard – FT3
Standard – FT4

Increased GT

3.375E-11 – TSH
3.375E-11 – FT3
3.375E-11 – FT4

Accordingly, hypothyroidism and hyperthyroidism present adaptive challenges to the homeostatic system to restore euthyroidism or at least ameliorate the dysfunctional state.

Resulting tornado plots show that the influence of various structure parameters on TSH level also depends on the overall function of the feedback loop, suggesting a distorted reaction in hypothyroidism or hyperthyroidism (see above). The overall relation appears to be modulated by additional regulatory loops other than the classical feedback control in the different functional states. Both the log TSH-FT4 analysis and the alternate model based on non-competitive divisive inhibition, while different in their methodological approach, yield comparable results.

Of notice:
For TSH – betaS is the most sensitive parameter

Clearance exponent for peripheral TSH is 2,3 x 10-4s-1 Calculated from plasma half-life of 50 min ([11 : Therefore, the elevated plasma TSH levels found in hypothyroidism are a result of both slower degradation and increase in rate of secretion.), 12])